Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - читать онлайн книгу. Автор: Джон Дербишир cтр.№ 37

Как нам измерить этот наклон и что это такое? Сначала давайте определим «наклон» наклонной прямой линии. Это подъем по вертикали, деленный на смещение по горизонтали. Если, пройдя по горизонтали расстояние в 5 единиц, вы поднялись на 2 единицы вверх, то, значит, наклон равен двум пятым, т.е. 0,4 (рис. 7.2).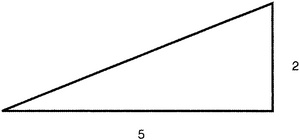

Чтобы найти наклон некоторой кривой в произвольной точке на ней, построим прямую линию, касающуюся кривой в выбранной точке. Ясно, что имеется ровно одна такая прямая. Если я слегка ее «покачаю» (можно представлять себе, что прямая — это стальной стержень, а кривая — стальной обод), то точка касания с кривой слегка сместится. Наклон кривой в данной точке — это наклон этой единственной касательной в этой точке. Для ln x наклон при аргументе x = 10, если вы его измерите, равен ¹/₁₀. Наклон при аргументе 20, конечно, меньше этого; измерение дает ¹/₂₀. Наклон при аргументе 5 больше — и измерение дает ¹/₅. На самом деле еще одно поразительное свойство логарифмической функции состоит в том, что при любом аргументе x ее наклон равен 1/x — числу, обратному x (обозначаемому еще как x⁻¹).

Если вы когда-нибудь слушали лекции по дифференциальному исчислению, то все это вам хорошо знакомо. Дифференциальное исчисление в действительности начинается с такого утверждения: из любой функции f можно произвести другую функцию g, которая выражает наклон функции f при любом ее аргументе. Если f — это ln x, то g — это 1/x. Произведенная таким образом функция называется, как ни странно, производной функции f. Например, 1/x — это производная функции ln x. Если вам дали какую-то функцию f, то процесс нахождения ее производной называется дифференцированием.

Дифференцирование — действие, которое подчиняется некоторым простым правилам. Например, оно прозрачно для нескольких основных арифметических операций. Если производная функции f — это g, то производная функции 7f — это 7g. (Так что производная от 7∙ln x равна 7/x.) Производная суммы f + g — это производная функции f плюс производная функции g. Правда, все не совсем так для умножения: производная произведения f и g не равна произведению производной функции f на производную функции g. ^[58]

Единственные функции, кроме логарифма, производные которых нам понадобятся в этой книге, — это простые степенные функции x^N. Приведем без доказательства тот факт, что для любого числа N производная функции x^N есть функция Nx^N−1. Таблица 7.1 дает некоторые производные степенных функций.

Функция	Производная
x−3	−3x−4
x−2	−2x−3
x−1	−x−2
x0	0
x1	1
x2	2x
x3	3x2

Конечно, x⁰ — это просто единица, а график этой функции — горизонтальная прямая. У нее нет наклона — точнее, нулевой наклон. Дифференцирование любого фиксированного числа дает нуль. А x¹ — это просто x, график же представляет собой прямую, идущую по диагонали вверх и покидающую рисунок через правый верхний угол. Наклон ее повсюду равен 1. Заметим, что нет такой степенной функции, производная которой была бы равна x⁻¹, хотя x⁰ вроде бы стоит на правильном месте, чтобы дать такую производную. Это неудивительно, поскольку мы уже знаем, что производная ln x есть как раз x⁻¹. Это еще одно свидетельство того, что ln x как будто пытается выдать себя за x⁰.

VII.

Вы, должно быть, помните мои слова о том, что математики обожают все обращать. Если задано выражение P через Q, то как выразить Q через P? Именно так мы исходно и получили логарифмическую функцию — как обращение показательной функции. Если a = e^b, тот как найти b через a? Как ln а.

Так вот, предположим, что мы продифференцировали функцию f и получили функцию g. То есть g представляет собой производную функции f. А f представляет собой… (что именно?!) функции g? В чем состоит обращение дифференцирования? Производная ln x — это 1/x, так что ln x — это… (что?) функции 1/x? Ответ: интеграл, вот что. Обращение производной — это интеграл, а обращение дифференцирования — это интегрирование. Поскольку вся эта деятельность прозрачна для умножения на фиксированное число, переворачивание таблицы 7.1 вверх ногами и некоторая ее «доводка» дадут нам обратную операцию, которая и представлена в таблице 7.2. И вообще, если только N не равно −1, то интеграл от функции x^N равен x^N+1/(N + 1). (Взгляд на таблицу еще раз показывает, как функция ln x изо всех сил старается вести себя как функция x⁰, каковой она, конечно, не является).

Функция	Интеграл
x−3	−1/2x−2
x−2	−x−1
x−1	ln x
x0	x
x1	1/2x2
x2	1/3x3
x3	1/4x4