
|
||
|
|
||
|
|
Онлайн книга - Путеводитель для влюблённых в математику | Автор книги - Эдвард Шейнерман
Cтраница 42

с² = 3² + 4² = 9 + 16 = 25. Таким образом,
В общем случае комплексное число a + bi задает точку с координатой a по горизонтали и координатой b по вертикали. Отрезок, соединяющий эту точку с началом координат, представляет собой гипотенузу прямоугольного треугольника с катетами длиной a и b. Если мы обозначим длину гипотенузы буквой c, то получим в соответствии с теоремой Пифагора: 
Необходимо отметить, что эта формула работает как для комплексных, так и для действительных чисел [154]. Например, если мы хотим вычислить абсолютную величину числа –4 сложным путем, представим его в комплексном виде: – 4 + 0i. Подставив a = –4 и b = 0 в формулу (A), мы получим: 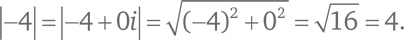
Пифагоровы тройки Если катеты прямоугольного треугольника равны 3 и 4, то гипотенуза равна 5. Все это целые числа [155]. Вот другой пример: если длины катетов 5 и 12, то длина гипотенузы – 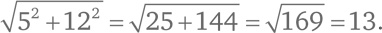
Все три числа снова оказались целыми. Но так везет не всегда. Если длины катетов – 2 и 3, то длина гипотенузы
Если три положительных целых числа a, b, c являются длинами сторон прямоугольного треугольника, их называют пифагоровой тройкой. Простейшие примеры: 3, 4, 5 и 5, 12, 13. А как насчет других? Как их отыскать? Удивительно, но факт: ключ к пифагоровым тройкам лежит в области комплексных чисел! Прежде чем погрузиться в детали, посмотрим, как комплексное число z = 2 + i связано с пифагоровой тройкой 3, 4, 5: • Шаг 1. Вычислим z²: z² = (2 + i) × (2 + i) = (4–1) + (2 + 2) i = 3 + 4i. • Шаг 2. Вычислим |z²|: 
Вычисления на шаге 2 показывают, что числа 3, 4 и 5 представляют собой пифагорову тройку. Отрезок на комплексной плоскости, соединяющий начало координат и точку 3 + 4i, – это гипотенуза прямоугольного треугольника со сторонами 3 и 4, ее длина равна 5. Повторим процедуру с комплексным числом z = 3 + 2i. Посчитаем z² и абсолютную величину этого числа: 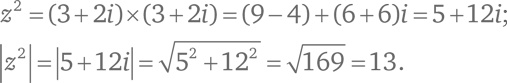
Мы нашли пифагорову тройку: 5, 12, 13! Еще один пример, и мы поймем принцип. Возьмем число z = 5 + 2i. Возведем его в квадрат и посчитаем абсолютную величину получившегося числа: 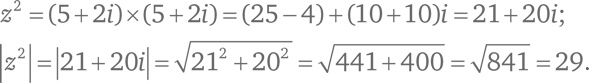
Мы нашли еще одну пифагорову тройку: 20, 21, 29. Давайте подумаем, как это работает, вернувшись к первому примеру: z = 2 + i. Заметим:
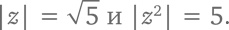
Таким образом, |z²| = |z|². Всегда ли так? Разумеется, тождество выполняется для действительных чисел (например, |(–4)²| = |16 | = |–4 |²), но доказательство этого факта для комплексных чисел потребует некоторых алгебраических выкладок (проделайте их самостоятельно и сверьтесь с решением в конце главы [156]). Вернемся к процедуре поиска пифагоровых троек. Начнем с комплексного числа z = x + yi, где x и y – целые числа
[157]. Абсолютная величина z может не быть целым числом, но оно представляет собой квадратный корень из целого числа:
z² = (x + yi) × (x + yi) = (x² – y²) + (2xy) i. Пусть a = x² – y², b = 2xy, c = x² + y². Тогда |a + bi| = c; следовательно, a² + b² = c². Последний пример: пусть z = 7 + 4i. Его квадрат равен 33 + 56i, абсолютная величина этого числа равна
|
 Вывод: |3 + 4i| = 5.
Вывод: |3 + 4i| = 5.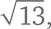 а это иррациональное число.
а это иррациональное число.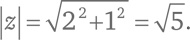 Мы возвели z в квадрат и посчитали абсолютную величину получившегося числа:
Мы возвели z в квадрат и посчитали абсолютную величину получившегося числа:
 Подытожим:
Подытожим: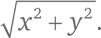 Абсолютная величина z² непременно будет целым числом: |z²| = |z|² = x² + y². Найдем z²:
Абсолютная величина z² непременно будет целым числом: |z²| = |z|² = x² + y². Найдем z²: Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно