Путеводитель для влюблённых в математику - читать онлайн книгу. Автор: Эдвард Шейнерман cтр.№ 22

Подытожим: у нас есть два способа доказать, что конечные множества имеют равные мощности: пересчитать их элементы или найти между ними взаимно однозначное соответствие. Однако, если множество содержит бесконечно много элементов, первый метод перестает работать: ни одно число не подходит на роль мощности ℝ (множество действительных чисел). Таким образом, нам остается лишь найти взаимно однозначное соответствие, чтобы показать, что мощности двух бесконечных множеств совпадают. Вот пример.

Как мы помним, буквой ℤ обозначается множество целых чисел:

Введем обозначение ℤ⁺ для множества положительных целых чисел ^[84]:

Совпадают ли мощности ℤ и ℤ⁺?

Есть искушение сказать, что ℤ содержит вдвое больше элементов, чем ℤ⁺ и потому «в два раза более бесконечно». Однако мощности данных множеств совпадают. Почему? Мы покажем это с помощью взаимно однозначного соответствия.

Составим два перечня. Первый будет включать все положительные целые числа, а второй – вообще все целые числа, и положительные, и отрицательные, но в необычном порядке. Сопоставляя числа в первом и втором перечне, мы выстроим взаимно однозначное соответствие. Это показано в таблице ^[85].

Таким образом, мощности ℤ и ℤ⁺ равны, что, в принципе, и неудивительно – ведь оба эти множества бесконечны.

Бесконечные множества разных мощностей

Выстроив взаимно однозначное соответствие между элементами двух множеств, мы показали, что мощности ℤ и ℤ⁺ совпадают, что они, так сказать, «одинаково бесконечны». Пришло время для вопроса поинтереснее: совпадают ли мощности ℤ⁺ и ℝ? Да, разумеется, оба бесконечны. Впрочем, лучше не утверждать наверняка, пока мы не выстроим взаимно однозначное соответствие между их элементами. Сейчас мы убедимся, что это невозможно.

Итак, мы должны сопоставить каждый элемент первого множества с элементом второго множества и убедиться, что каждый элемент второго множества сопоставлен с элементом первого. Как же доказать, что это невозможно? Мы покажем, что попытки выстроить все элементы ℤ⁺ и ℝ в пары обречены на провал, потому что кое-какие элементы ℝ окажутся пропущены. А теперь к делу!

Допустим, мы все-таки нашли взаимно однозначное соответствие между ℤ⁺ и ℝ. Тогда все элементы можно занести в таблицу такого рода: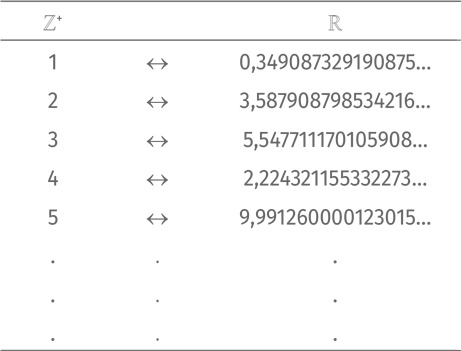

Все целые положительные числа занесены в левую колонку, все (вроде бы) действительные числа занесены в правую колонку. Сейчас мы убедимся: как ни заполняй правую колонку, будут действительные числа, которые туда не попадут.

Но прежде нам придется отвлечься на одну досадную техническую проблему ^[86]. Некоторые действительные числа в десятичной системе счисления записываются двумя способами. Например, число 1/4. С одной стороны, мы можем записать его как 0,25. С другой стороны, можно записать и так: 0,24999999999999… Ряд девяток уходит в бесконечность. 0,25 тоже можно записать с бесконечным количеством нулей на конце. Таким образом,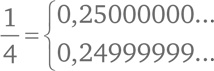

Примем решение вносить в таблицу запись числа с нулями на конце. Это никак не влияет на доказательство, мы просто договариваемся о форме записи.

Итак, вернемся к доказательству. Представим, что перед нами уже лежит таблица с колонками целых положительных и действительных чисел. Поищем действительное число, ускользнувшее из правой колонки.

Для начала подчеркнем первую цифру после запятой в первой колонке, вторую цифру после запятой во второй колонке и т. д.: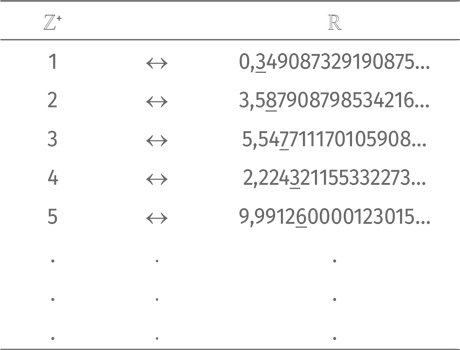

Выпишем подчеркнутые цифры в ряд: 3, 8, 7, 3, 6… С помощью этого ряда создадим новое число. Начнем его с нуля, поставим десятичную запятую и дальше будем двигаться по ряду подчеркнутых цифр с двумя условиями:

(A) Если подчеркнута цифра 3, пишем 7.

(B) Если подчеркнута не цифра 3, пишем 3.

Как это работает с нашим рядом?

Первая цифра 3. Выполняется условие (A). Мы получаем 0,7___.

Вторая цифра 8. Выполняется условие (B). Мы получаем 0,73___.

Третья цифра 7. Снова выполняется условие (B). Получаем 0,733___.

Четвертая цифра снова 3, по правилу (A) ставим семерку: 0,7337___.

Пятая цифра 6, по правилу (B) ставим тройку: 0,73373___.

Продолжая двигаться вдоль ряда подчеркнутых цифр, мы получим число x. В нашем примере число x = 0,73373…, а остальные цифры заполняются согласно условиям (A) и (B).

Вот процесс выстраивания x в пошаговом виде:

Число x зависит от нашей таблицы. Другая таблица даст другое x. Мы утверждаем, что в любой таблице x, выстроенное таким образом, не встречается в правой колонке; следовательно, взаимно однозначное соответствие между целыми положительными и действительными числами невозможно.

Начнем с самого верха. Очевидно, число x не идентично первому числу в правой колонке, и вот почему. Первая строка 1 ↔ Y₁. Если первая цифра Y₁ после запятой – тройка, то первая цифра числа x после запятой – семерка; но если первая цифра Y₁ после запятой – не тройка, то первая цифра числа x после запятой, напротив, – тройка. Ситуация выглядит так: