
|
||
|
|
||
|
|
Онлайн книга - Путеводитель для влюблённых в математику | Автор книги - Эдвард Шейнерман
Cтраница 15

Какое комплексное число взаимно обратно 1 + 2i? Нам нужно такое число a + bi, что (1 + 2i) × (a + bi) = 1. Докажем, что этому требованию удовлетворяет число

Общая формула для комплексного числа, обратного числу a + bi, выглядит следующим образом: 
В этом легко убедиться: достаточно умножить (A) на a + bi, аккуратно произвести все необходимые арифметические действия – и получить в итоге единицу. Заметим, что оба знаменателя в (A) равны a² + b². Если вдруг эта сумма окажется равной нулю, формула потеряет смысл, потому что деление на ноль запрещено. Но такое возможно лишь в том случае, если a = 0 и b = 0. Другими словами, все комплексные числа имеют взаимно обратные, кроме числа 0 + 0i. Это подтверждает ожидания: ноль – единственное действительное число, не имеющее взаимно обратного, и среди комплексных чисел дело обстоит так же. Но обратное по отношению к любому ненулевому комплексному числу – тоже комплексное число. Расправившись со взаимно обратными числами, мы можем наконец перейти к делению. Деление числа X на число Y дает такой же результат, как умножение числа X на число, взаимно обратное Y. Следовательно, частное двух комплексных чисел (если делитель не равен нулю) – комплексное число. Отсюда можно сделать вывод: основные арифметические действия – сложение, вычитание, умножение и деление – прекрасно справляются с комплексными числами. Мы можем проделать эти операции над парой любых комплексных чисел (исключение составляет деление на ноль) и получить комплексное число. Сейчас мы снова попытаемся извлечь квадратный корень. Сперва именно эта задача загнала нас в тупик. Действительные числа, так сказать, неполноценны: из каких-то квадратный корень извлекается, а из каких-то – нет. И вот мы дополняем действительные числа мнимыми, придумав новое число
К счастью, множество комплексных чисел уже содержит все квадратные корни из комплексных чисел. Посмотрим, как извлечь корень из мнимой единицы, не создавая новых сущностей. Нам нужно найти такое комплексное число a + bi, что (a + bi) ² = i. Начнем с перемножения (a + bi) и (a + bi): (a + bi) × (a + bi) = (a² – b²) + (2ab) i. Теперь нам нужно приравнять это выражение к i = 0 + 1 × i. В результате мы получим: a² – b² = 0 и 2ab = 1. Первое условие тождественно тому, что a = b или a = –b. Если a = b и 2ab = 1, то 2a² = 1. Таким образом,
Так как a = b, мы нашли два квадратных корня из мнимой единицы: 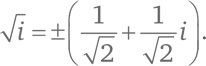
Проверьте, так ли это, возведя оба ответа в квадрат. Если a = –b, решение будет таким же. Итак, затратив некоторые усилия, мы показали, что извлечение квадратного корня из комплексного числа дает комплексное число, поэтому придумывать новые числа для извлечения корней не нужно. Основная теорема алгебры А как насчет кубических корней? Кубический корень из числа c – это такое число x, что x³ = c. Вопрос: входит ли множество корней из комплексных чисел во множество комплексных чисел или нам нужно изобретать еще какие-нибудь новые числа [59]? Уравнение x³ = c может быть записано иначе: x³ – c = 0. Сформулируем вопрос в общем виде: всякое ли полиномиальное уравнение [60] имеет решение среди комплексных чисел? Скажем, есть ли такое комплексное число x, что 3x⁵ + (2 – i) x⁴ + (4 + i) x³ + x – 2i = 0? Принципиально важный факт в теории комплексных чисел состоит в том, что любое полиномиальное уравнение имеет комплексное решение! Об этом говорит основная теорема алгебры. На математическом языке данный тезис можно переформулировать так: поле комплексных чисел [61] алгебраически замкнуто. Вот как звучит это важнейшее утверждение в строгой форме. Теорема (основная теорема алгебры). Пусть d – положительное целое число и c0, c1, c2, …, cd – комплексные числа, причем cd ≠ 0. Тогда существует такое комплексное число z, что cdzd + cd – 1zd – 1 + … + c2z² + c1z + c0 = 0.
|
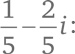
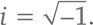 Мы заново осваиваем арифметические операции, и система действительных чисел разрастается до системы комплексных чисел
Мы заново осваиваем арифметические операции, и система действительных чисел разрастается до системы комплексных чисел
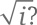 Нам что, опять нужно изобрести какое-то несуществующее число и создать монструозное множество «сверхкомплексных» чисел?
Нам что, опять нужно изобрести какое-то несуществующее число и создать монструозное множество «сверхкомплексных» чисел?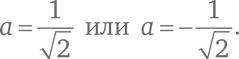
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно