Математика и криптография. Тайны шифров и логическое мышление - читать онлайн книгу. Автор: Роман Душкин cтр.№ 3

7. К таблице, которую мы заполняли на шаге 4, необходимо пририсовать ещё один столбец. В него мы будем записывать расшифровки символов.

Так, повторяя шаги 5 и 6, ты сможешь расшифровать весь текст. Однако иногда предположения относительно соответствия символов могут оказаться неверными. Это часто происходит, когда разгаданных символов ещё не так много, чтобы уже можно было видеть целые слова, а частоты разгадываемых символов примерно одинаковы. Тогда надо делать шаг назад в рассуждениях и выносить иное предположение. Также возможно, что в шифрограмме намеренно снижены или повышены частоты некоторых букв, и это может ввести в заблуждение. Но грамотный криптоаналитик в конце концов расшифрует и такой текст.

Давай попробуем разгадать по этому алгоритму ту шифрограмму, которая приведена несколькими страницами раньше. А после этого ты сможешь самостоятельно сделать то же самое с любой другой шифрограммой, текст в которой зашифрован этим способом, но, возможно, при помощи других значков.

Итак, в шифрограмме 419 букв (если твой результат отличается на пару букв, это не страшно, поскольку такая неточность не повлияет на результаты. А вот если ты ошибёшься на десяток букв, то тут уже придётся пересчитывать).

Теперь начнём считать частоты символов. В результате должна получиться примерно такая таблица:

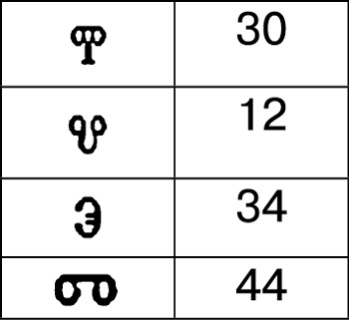
Надеюсь, что ты заполнишь все остальные строки самостоятельно.

После того как таблица будет построена, строчки необходимо отсортировать по убыванию количества символов. Если это сделать, то в результате получится что-то вроде этого: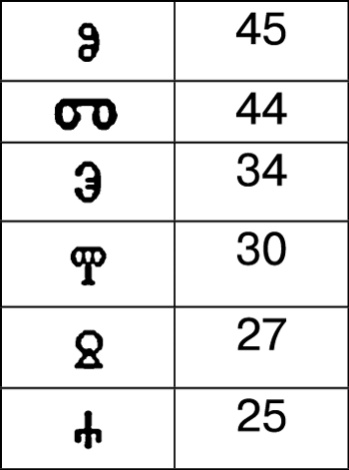

Как видно, здесь частота первых двух символов отличается только на единицу. Это очень неприятная ситуация, поскольку придётся делать гипотезы и проверять их. Впрочем, криптоаналитик при дешифровке всегда строит гипотезы и пытается их проверить. Так что давай сейчас построим одну гипотезу. Поскольку самой частой буквой в русском языке является «О», то предположим, что значок из первой строки отсортированной таблицы — это и есть буква «О». Что получится, если в соответствии с догадкой подставить эту букву в наш текст? Вот:

−−−−−−. −−−−−−−, −−О −−−−−−−−−О−−−−−О−−, −−−−−−−−−−−−О−−−−−−. −−−−−−О −−−, −О −−О−−−О−−−−−−−−О−О−. −−−−−−−−−−−−О−−−−−−−, −−−−−−О−−О−−О−−−−−О−−−−О−−−−−−−О −−−О−−−−−−−−−−−−−−−−−−−−−−−−−−−−О−. −О−−О−−−−−О−−−−−−−−О−−−−−−−. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−, −−−−О−−О −−−−−−О−−−−−−О−−О−−−−−−−−−, −−О−−−−−−О −−−О−−−−−−−−−−− (−−О−−−−−, −О−−−−−О−−−−−−−−О−−−−−−−−). −−О −−−−−−−О−−О, −−−−−О −О−−−−−−−−−−−−−−−−−−−−−−−−, −−О−О −−−−−−−−−−−−−−−−−−−−−−−−−О−−О−−−−−−О.

Не очень-то понятно. Тем не менее это уже что-то.

Что делать дальше? Теперь попробуем подставить следующую по частоте букву. Для русского языка это буква «Е», так что подставим её вместо символа, занимающего вторую строчку в отсортированной таблице. Вот что получится после этого:

−−−−−Е. −−−−−−−, −ЕО − Е−−−−−−−О−−−−−О−−, − Е−−−Е−−−−−ЕОЕ Е−−−Е. −−−−−ЕО Е−−, ЕО −−О−−−О−−−Е−−− ЕО−О−. −−− Е− Е−−−−−−О−−−−−−−, −−−−−−О−ЕО−−О−−Е−−О−−−−О−−−−−−−О −−−О−−Е−−−−−−−−−−−−−− Е−−−−−−−−−ЕО−. −О−ЕО−−−−−О−−−−−−−−О−−−−−−−. − Е−−−−−−−−Е−−−−−−−−−−−Е−− Е−−−−−−−−, −−−−О−−О −−−−−−О−−Е−−−О−−О−−−−−− Е−−, −ЕО−−−−−ЕО −−−О−−−−−−−−−Е− (−−О−− Е−−, −О−− Е−−О−−−−−−−−О−−−−−−Е−). −ЕО −− Е−−−−О−−О, Е−−−ЕО −О−−−−−−−−−−−−−−− Е−−−−−−−−, −−О−О Е−−−−−−−−−−−−−Е−−−−−Е−−−−О−ЕО−Е−−−−О.