Математика и криптография. Тайны шифров и логическое мышление - читать онлайн книгу. Автор: Роман Душкин cтр.№ 28

Для удобства и ускорения работы можно сделать таблицу размером 32 × 32 ячейки: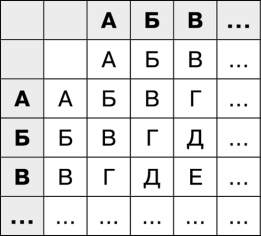

По такой таблице сразу видно, что сложение букв «Б» и «В» даёт букву «Д» (ищем ячейку на пересечении «Б» и «В», причём неважно, в строке или в столбце стоят буквы, поскольку операция коммутативна) и т. д.

Теперь надо выполнить две несложные задачи:

1. Придумать сообщение, длина которого должна быть не менее 500 символов.

2. Придумать ключ длиной в четыре символа. Если ключ короче четырёх символов, то шифрограмму будет взломать очень просто, а более длинные ключи сделают работу юного криптоаналитика слишком сложной, и он, скорее всего, отставит эту задачу и это занятие как слишком утомительное. В целях обучения я крайне рекомендую в качестве ключа использовать какое-либо слово, знакомое ребёнку, а не случайное сочетание букв.

3. Зашифровать придуманное сообщение при помощи процедуры сложения с ключом.

Всё ранее описанное можно осуществить при помощи арифметики вычетов по модулю 32. Если каждому символу алфавита от пробела до буквы «Я» поставить в соответствие число от 0 до 31, то в совокупности с арифметическими операциями сложения и вычитания получится кольцо Z³². Тогда шифрование будет представлено в этом кольце как сложение кодов символов открытого текста и ключа, а дешифровка как вычитание кодов символов ключа из символов шифрограммы соответственно.

Давайте попробуем сделать такую шифровку. Здесь не будет открытого текста длиной не менее 500 символов, используем более короткий. Пусть это будет текст: «ХОРОШО ТЕМ КТО НАУЧИЛСЯ ШИФРОВАТЬ СООБЩЕНИЯ ХОРОШО», а ключом пусть будет слово «ШИФР». Как видно, здесь не используются знаки препинания. В принципе, они никогда не используются при шифровании, поскольку избыточны.

Начнём: Х + Ш = О. О + И = Ч. Р + Ф = Е. О + Р = ПРОБЕЛ. Ну и так далее. В итоге получается шифрограмма: «ОЧЕ СЧФГЯХФЫЛЧФЯЩЭМЩДЪУРССЙБЗЛХГФИЖ ЗКОЦЖСУРОЧЕ СЧ». Уже на этом простом примере видно, что такой шифр намного сложнее, чем использованный на прошлой неделе.

Шифрограмму, полученную описанным методом, необходимо вставить во второе письмо для юного криптоаналитика. Соответственно, можно написать что-то открытым текстом, а в него вставить подготовленную шифрограмму. Письмо отправляется обычным порядком. Скорее всего, ребёнок испытает определённые сложности с расшифровкой послания, поскольку это дело достаточно трудоёмкое, так что рекомендую сразу готовиться к тому, чтобы объяснить ребёнку суть метода, способ шифрования и дешифровки, а также совместными усилиями дешифровать полученную шифрограмму.

Теперь предлагаю изучить один очень занятный метод стеганографии (и криптографии одновременно). Этот метод переворачивает сознание у тех, кто впервые о нём узнаёт, хотя, по сути, он очень прост. Но переворот сознания необходим тем, кто старается познать тайны криптографии, поэтому мы должны рассмотреть этот метод.

Что такое стеганография? Это набор методов и практик сокрытия сообщений. Основная цель стеганографии заключается в том, чтобы скрыть сам факт передачи тайного сообщения. Другими словами, тайное сообщение как бы прячется. Оно даже может быть не шифрованным. Но если спрятанное сообщение ещё и зашифровать каким-нибудь способом, то степень защиты будет повышена, особенно если метод шифрования нарушает частоты распределения символов в шифруемом тексте. Тогда найти стеганограмму намного сложнее, поскольку она начинает выглядеть как «шум». Непосвящённый человек не сможет выявить её, а у криптоаналитика будет очень мало зацепок, чтобы попытаться обнаружить стеганограмму (например, статистическими методами).

В течение третьей недели мы научимся скрывать сообщение методом, который придумал английский философ и математик Фрэнсис Бэкон. Мы немного изменим его метод и применим его для русского языка. В итоге получится очень интересная вещь, которой можно пользоваться в любых областях жизни. Начнём же…

Помните, я не зря упомянул о том, что в нашем новом алфавите ровно тридцать два символа. Число 32 для криптографов и математиков — «круглое», поскольку в двоичной системе счисления записывается как «100000». Другими словами, для представления тридцати двух символов нам требуется 5 бит информации, поскольку 32 = 2⁵. Мы можем воспользоваться этим для нового способа кодирования символов нашего алфавита: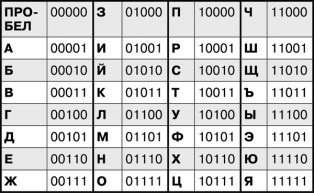

Тот из читателей, кто изощрён в информатике или программировании, уже понял, что это двоичный код для всех тридцати двух символов. Другими словами, каждому символу из алфавита ставится в соответствие пятизначное двоичное число, то есть число, состоящее ровно из пяти цифр 0 или 1. При этом нули на первых местах не удаляются, как мы это привыкли делать в десятичной системе. Здесь особенно важно, чтобы длина кода для каждого символа была равна пяти.

Соответственно, чтобы зашифровать текст, необходимо выписать один за другим код каждого символа. Например, пусть есть текст «ПОДГОТОВЬ ИНГРЕДИЕНТЫ К МОЕМУ ПРИЕЗДУ». Этот текст шифруется при помощи представленного выше кода так:

10000011110010100100011111001101111000111101100000010010111000100100010011000101 01001001100111010011111000000001011000000110101111001100110110100000001000010001 0100100110010000010110100

А теперь самое главное. Пустьцифра 0 обозначаетобычную букву, а цифра 1 — жирную. Весьэтот код можно «нанести» на произвольный текст при помощитакогосоответствия. И, самое главное, необязательно использовать свойство жирности символа, для этих целей подойдёт любое двоичное свойство: большая буква или маленькая буква, прямая или курсив, красного цвета или чёрного. Можно даже использовать такие свойства, как «находится в первой половине алфавита или во второй» или «находится на чётном месте в алфавите или на нечётном». Но эти два последних свойства сложнее, при помощи их спрятать код можно не в любом тексте.

Как видно, эта же шифрограмма «нанесена» на обычные слова в начале предыдущего абзаца, при этом использовались все символы для нанесения (то есть и цифры, и знаки препинания). Неподготовленный читатель даже не обратит внимания на такое странное начертание текста. Но грамотный криптоаналитик, конечно же, всё сразу поймёт, этим никого не удивишь. Поэтому обычно используют более тонкие свойства, которые не так тривиальны и не видны невооружённым глазом.