
|
||
|
|
||
|
|
Онлайн книга - Стратегии решения математических задач. Различные подходы к типовым задачам | Автор книги - Стивен Крулик , Альфред Позаментье
Cтраница 31

Задача 7.11
Какое число в следующем ряду самое большое и какое число стоит на втором месте по величине? 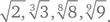
Обычный подход
В наши дни рука автоматически тянется к калькулятору. Однако найти ответ может быть не так просто, как кажется, поскольку не все калькуляторы могут извлекать такие корни. Образцовое решение
Сначала для удобства представим члены заданного ряда в виде степеней с дробными показателями: 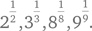
Эффективной стратегией здесь является организация данных так, чтобы было легко сравнивать. 
Задача 7.12
У класса есть возможность принять участие в походе. Желающих оказалось пять человек, а свободных мест — всего три. В числе желающих — Аманда, Билл, Кэрол, Дэн и Эван. Учитель взял пять листочков бумаги, каждый с именем одного из желающих, положил их в шляпу и вытащил три листочка наугад. Какова вероятность того, что Аманда, Билл и Кэрол попадут в число участников похода? Обычный подход
Сначала определим, сколько вариантов выбора может существовать. Порядок не имеет значения, поэтому это комбинаторная задача. Из пяти листочков выбирают по три за раз: 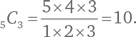
Поскольку Аманда, Билл и Кэрол могут выпасть только один раз, ответ
Образцовое решение
Если вы не знакомы с комбинаторными вычислениями, то можете воспользоваться стратегией организации данных. Составим перечень всех возможных сочетаний имен в любом порядке: 
Существует 10 возможных вариантов выбора трех человек. Только один из них, а именно ABC, удовлетворяет условиям задачи. Таким образом, правильным ответом будет один из 10, или
Глава 8
Схематичное изображение, или Визуальное представление Когда вопросы в задаче касаются определенной геометрической фигуры или рисунка, без слов понятно, что построение схем, или визуальное представление, является неотъемлемой частью метода решения. Это необходимо и помогает решить задачу. Довольно трудно представить, чтобы математики в далекие времена оперировали геометрическими понятиями без рисунков или хотя бы демонстрировали свои геометрические расчеты без использования чертежа. Вместе с тем есть множество задач, где условия не предполагают построения чертежа, однако визуализация того, о чем идет речь, намного облегчает поиск решения. Многие люди лучше воспринимают информацию визуально — чтобы понять происходящее, им нужна картина, а не просто слова. Это не домыслы. Визуализация — очень сильный метод, помогающий вникнуть в данную ситуацию. Например, когда нужно объяснить, как найти чей-то дом, схема направления движения просто неоценима. Рисунок помогает увидеть маршрут в целом. В журналах и газетах постоянно используются графики и другие визуальные инструменты для сравнения или противопоставления ситуаций. Когда вы покупаете что-то и должны собрать это сами, в руководстве производителя помимо письменных инструкций обычно приводятся рисунки. В большинстве видов спорта, особенно в футболе и баскетболе, тренер объясняет стратегию игры, как правило, с помощью диаграмм, или рисунков с крестиками и ноликами. Все это примеры повседневного использования стратегии схематичного изображения, когда напрямую оно не требуется. В конце концов, не зря же говорят, что лучше один раз увидеть, чем 100 раз услышать. Возьмем для примера математическую задачу, в которой изначально мало кто ожидает использования визуального представления. У г-на Адамса есть два теста в запасе для выпускного экзамена по алгебре, которые он хочет использовать в двух классах. В каждом тесте 26 разных вопросов. Он берет первые четыре вопроса из теста 1 и добавляет их в конец теста 2. Затем он берет четыре первых вопроса из теста 2 и добавляет их в конец теста 1. В каждом тесте теперь 30 вопросов. Сколько одинаковых вопросов в обоих тестах? Ситуацию до и после перестановок можно представить схематично, или визуализировать ее: 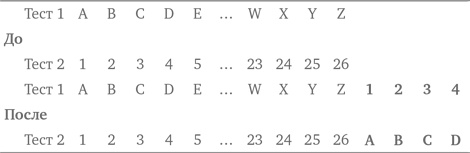
Теперь видно, что тесты содержат восемь одинаковых вопросов, а именно 1, 2, 3, 4 и A, B, C, D. Хотя в этом случае не обязательно использовать визуальное представление, и задачу можно решить другими методами, создание схемы позволяет увидеть, что происходит. Такой подход облегчает поиск решения. Имейте в виду, когда мы говорим о визуальном представлении, не обязательно подразумевается «вычерчивание» чего-либо. Вот еще одна задача, где визуальное представление помогает увидеть происходящее. Длина стороны равностороннего треугольника равна 40 см. Средние точки сторон соединяются так, что образуется второй равносторонний треугольник. Средние точки сторон этого треугольника соединяются так, что образуется третий треугольник. Этот процесс продолжается до тех пор, пока мы не получим пять треугольников. Чему равен периметр пятого треугольника? |
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно