Интерстеллар: наука за кадром - читать онлайн книгу. Автор: Кип С. Торн cтр.№ 45

Существует ли балк на самом деле, в реальности, или это лишь плод нашего воображения? Вплоть до восьмидесятых большинство физиков, включая меня, считали балк вымыслом.

Но как же может он быть вымыслом? Разве мы не знаем наверняка, что наше пространство искривлено? Неужто обмен радиосигналами с аппаратами «Викинг» не подтвердил это искривление с высокой точностью (см. главу 4)? Подтвердил… А раз наше пространство искривлено, разве не должно оно прогибаться в некое пространство с большим количеством измерений – в балк?

Нет, не обязательно. Вполне возможно, чтобы наша Вселенная искривлялась и без участия многомерного балка. Мы, ученые, можем выразить искривление нашей Вселенной математически, не привлекая для этого балк. Формулировать законы теории относительности, которые управляют искривлением, можно без участия балка. В сущности, именно так почти всегда мы и поступаем. До восьмидесятых балк был для нас не более чем вспомогательным построением. Построением, позволяющим лучше понять смысл наших расчетов, а также общаться на эту тему друг с другом и с людьми, далекими от физики. Итак, вспомогательное построение, а не явление реальности.

Но что значит «реальный балк»? И как мы можем проверить его реальность? У нас были бы доказательства существования балка, если бы он влиял на наши измерения. И до восьмидесятых мы не видели, каким образом это может происходить.

Но в 1984 году все изменилось, и изменилось в корне. Майкл Грин из Лондонского университета и Джон Шварц из Калтеха совершили революцию в области квантовой гравитации ^[66]. Однако – вот так сюрприз! – их рассуждения имели смысл лишь при условии, что наша Вселенная – это брана, находящаяся в балке, у которого одно временное и девять пространственных измерений. То есть в балке, у которого на шесть пространственных измерений больше, чем у нашей браны. Согласно так называемой теории суперструн, которой следовали Грин и Шварц, высшие измерения балка влияют на нашу брану различными способами и, когда человеческие технологии достигнут определенного уровня, эти влияния можно будет измерить в ходе физических экспериментов. И, возможно, это позволит совместить законы квантовой физики с законами эйнштейновской теории относительности.

Рис. 21.2. Слева: Майкл Грин (слева) и Джон Шварц (справа) путешествуют автостопом, Аспен, штат Колорадо, 1984. Справа: Майкл Грин (крайний слева) и Джон Шварц (крайний справа) в 2014 году получают за свое открытие премию по фундаментальной физике размером в три миллиона долларов. На заднем плане – Юрий Мильнер (учредитель премии) и Марк Цукерберг (соучредитель социальной сети «Фейсбук»)

С момента суперструнной революции Грина – Шварца мы, физики, воспринимаем теорию суперструн очень серьезно и прилагаем много усилий к ее развитию. И, соответственно, мы всерьез воспринимаем идею, что балк существует и может оказывать влияние на нашу Вселенную.

Хоть теория суперструн и утверждает, что у балка на шесть измерений больше, чем у нашей Вселенной, удобнее принять, что дополнительное измерение всего одно (подробнее об этом в главе 23).

Поэтому, а также потому, что шесть дополнительных измерений – это как-то чересчур для фильма, рассчитанного на широкую аудиторию, в «Интерстеллар» балк обладает лишь одним дополнительным измерением, а всего их выходит пять. Балк делит с нашей браной три ее пространственных измерения: «восток – запад», «север – юг» и «верх – низ». И кроме того, он обладает четвертым пространственным измерением, «туда – обратно», которое простирается перпендикулярно нашей бране, над и под ней, как на рис. 21.3.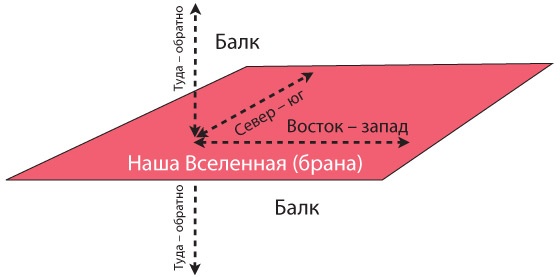

Рис. 21.3. Наша Вселенная как брана с четырьмя пространственно-временными измерениями, находящаяся в пятимерном балке. Два измерения – время и «верх – низ» – здесь опущены

Измерение «туда – обратно» играет важную роль в фильме, хотя профессор и другие персонажи не называют его так, говоря просто о «пятом измерении». «Туда – обратно» – центральное понятие для следующих двух глав, а также для глав 25, 29 и 30.

В 1844 году Эдвин Эбботт написал сатирический роман под названием «Флатландия». Хоть сатира на викторианскую культуру в этом романе и кажется старомодной, а отношение к женщинам – возмутительным, само место действия книги имеет прямое отношение к «Интерстеллар», и я очень ее вам рекомендую.

Рис. 22.1. Обложка первого издания «Флатландии»

Роман повествует о приключениях сущности, имеющей форму квадрата и живущей в двумерной вселенной – Флатландии. Квадрат посещает одномерную вселенную, называемую Лайнландией, нульмерную вселенную – Пойнтландию, и, что производит на него особо сильное впечатление, трехмерную вселенную – Спейсландию ^[67]. Кроме того, когда Квадрат живет во Флатландии, его посещает сферическая сущность из Спейсландии.

При нашей первой встрече с Кристофером Ноланом мы с радостью обнаружили, что оба знаем и любим роман Эбботта.

Представьте что вы, подобно Квадрату в романе Эбботта, – двумерная сущность, живущая в двумерной вселенной, напоминающей Флатландию. Ваша вселенная может быть поверхностью стола, или листком бумаги, или резиновой мембраной. В традициях современной физики я буду называть ее двумерной браной.

Получив хорошее образование, вы предполагаете существование трехмерного балка, в котором находится ваша брана, но вы в этом не уверены. Представьте свою радость, когда однажды вас посетит сфера из трехмерного балка. «Сущность из балка» – так вы могли бы ее называть.

Сначала вы не понимаете, что это сущность из балка, но понаблюдав за ней и хорошенько подумав, не находите иного объяснения. А наблюдаете вы следующее: внезапно, без предупреждения и непонятно откуда, на вашей бране возникает синее пятно (рис. 22.2 сверху слева). Пятно разрастается, превращаясь в синюю окружность, диаметр которой увеличивается до максимального (рис. 22.2 посередине слева), а затем снова сжимается в точку (рис. 22.2 снизу слева) и, наконец, полностью исчезает.