Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 52

^{Синусоидальная форма волны}

Для любой взятой синусоиды расстояние от некоторой произвольной точки до следующей такой же — величина постоянная. Эта длина (для простоты возьмем длину от гребня до гребня) определяет «длину волны». Длина волны обычно обозначается греческой буквой «лямбда» (λ).

Если узлы не отличаются друг от друга (а в физике они обычно не различаются), то расстояние между последовательными узлами равно половине длины волны (полуволне). Если восходящий узел одной волны при наложении совпадает с нисходящим узлом другой волны (такое иногда тоже случается), то говорят, что волны находятся «в противофазе», но расстояние между последовательными узлами все равно составляет половину длины волны.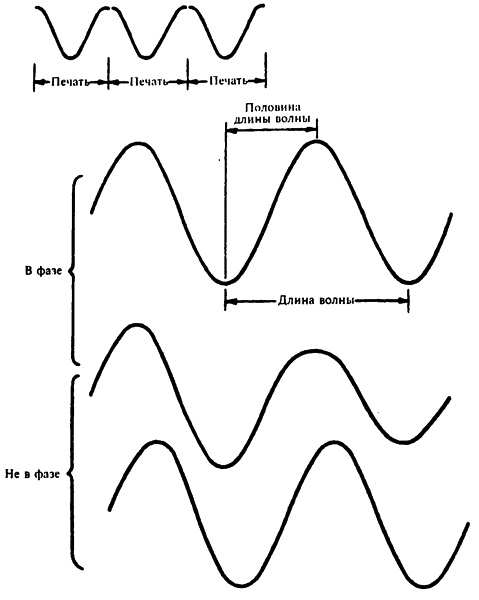

^{Длина волны}

В данной волне гребень двигается по направлению наружу по поверхности воды (хотя вода непосредственно, хочу повторить, не двигается наружу вместе с ним); расстояние, которое он проходит за одну секунду, называется скоростью распространения волны.

Давайте представим себе, что скорость распространения данной волны составляет десять метров в секунду и что длина волны (то есть расстояние от гребня до гребня) равняется двум метрам. Если мы обратим наше внимание на некоторую точку на поверхности воды, мы увидим, что в ней через некоторое время образуется гребень. Он начинает перемещаться, и, когда он переместится на два метра по направлению наружу, его место займет второй гребень, еще два метра вперед, и в точке появится третий гребень и так далее. После того как пройдет одна секунда, первоначальный гребень окажется на расстоянии в десять метров, а его место займет пятый гребень (10 разделить на 2).

Количество гребней (или количество впадин, восходящих узлов, нисходящих узлов или любых других последовательных точек в фазе), которые прошли через данную точку за одну секунду, называется «частотой колебаний» волны. Частота обычно обозначается греческой буквой «ню» (ν).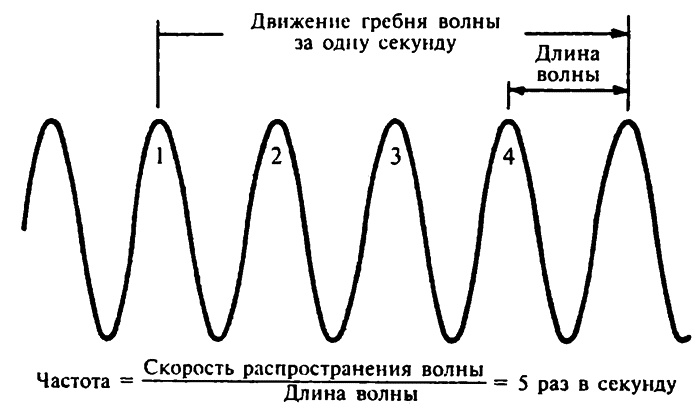

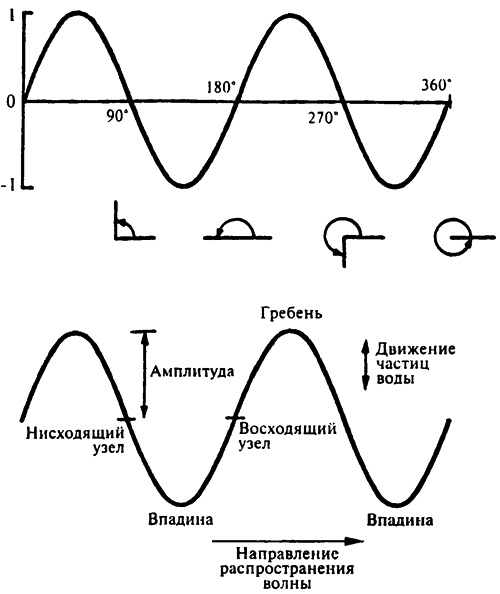
^{Частота колебаний волны}

Из того, что я только что сказал, должно быть ясно, что скорость распространения волны, поделенная на ее длину, равняется частоте ее колебаний, то есть:

ν = V/λ. (Уравнение 11.1)

Единицы измерения скорости в системе МКС — метры в секунду, единицы измерения длины волны — метры. Поэтому единицы измерения частоты получаются равными (м/с)/м, или 1/с. Поскольку в алгебре 1/a называется величиной, «обратной» a, величину 1/с иногда называют «обратными секундами». Более часто, конечно, мы просто говорим «в секунду». Например, частота упомянутой выше волны может быть записана как 5/с и читаться как «5 раз в секунду» или как «5 обратных секунд».

Еще на сравнительно ранней стадии развития поисков знания у исследователей возникли мысли о том, что звук представляет собой один из видов волнового движения. Впервые эксперименты со звуком начали проводить еще древние греки, и замечательно то, что созданная ими для изучения звука ветвь физики с самого начала развивалась в правильном направлении даже с точки зрения современных критериев.

Уже в VI столетии до н.э. Пифагор Самосский изучал звук, который издают струны. Как мы можем заметить, если струну «ущипнуть», то она начинает вибрировать. Движения струны выглядят как размытое пятно, но даже в этом случае можно получить некоторые полезные факты, связанные со звуком. Похоже на то, что ширина этого размытого пятна, созданного движением струны, соответствует громкости звука. По мере того как вибрация утихает, а ширина пятна сужается, звук становится менее громким. А когда вибрация прекращается, не важно — естественным замедлением или резкой остановкой струны рукой, — звук также прекращается. Кроме того, легко выяснить, что чем короче натянутая струна, тем более быстро она вибрирует, и более быстрая вибрация, как кажется, производит более пронзительный звук; в то же время более длинная струна, как кажется, вибрирует медленнее, а звук издает более низкого тона.

В 400 году до н.э. Архит Тарентский (ок. 420–365 до н.э.), член пифагорейской школы, предположил, что звук производится благодаря соударению тел — быстрое движение порождает высокий тон, а медленное движение — низкий тон. Примерно в 350 году до н.э. Аристотель предположил, что вибрирующая струна ударяет по воздуху и что та часть воздуха, которая была подвержена удару струны, в свою очередь, перемещается от удара, чтобы ударить соседнюю часть, которая, в свою очередь, ударяет следующую часть и так далее. Аристотель далее пришел к выводу, что воздух является средой, необходимой для того, чтобы звук распространялся, и что в безвоздушном пространстве никакого распространения, а значит, и самого звука не будет. (И в этом Аристотель был, несомненно, прав.)

Поскольку вибрирующая струна, двигаясь в быстром темпе, ударяет воздух не однажды, а многократно, то воздух должен провести не один удар, а целый длинный ряд ударов. Римский архитектор Витрувий, живший в I столетии до н.э., предположил, что воздух просто не двигается, а вибрирует и что он ведет себя таким образом в ответ на колебания струны. Он утверждал далее, что именно эти воздушные колебания мы и слышим как звук.

Ну и наконец, приблизительно в 500 году н.э. римский философ Северин Боэций (480–524?) сделал сравнительную аналогию проводимости звука сквозь воздух с волнами, которые возникают в спокойной воде от брошенного туда камня. Несмотря на то что данная аналогия достаточно справедлива и до сих пор можно рассматривать распространение звука в воздушной среде именно таким образом (и именно так, например, мы рассматриваем его в этой книге), все-таки следует отметить, что такой подход надо рассматривать только как предварительный, потому что между жидкостными волнами и звуковыми волнами на самом деле имеются достаточно важные различия.

Поперечные волны, типа жидкостных волн, могут появляться только при некоторых определенных условиях. Эти волны представляют собой такие состояния тел, при которых одна часть тела (а точнее — его поперечное сечение) перемещается боком относительно другой части, а затем совершает такое же движение, но в противоположную сторону. (Можно воспроизвести поперечную волну, если взять очень высокую стопку карт и переместить каждую карту вбок на нужное расстояние.) Такое поперечное движение производится определенным типом силы, называемым «сдвиг». Но для того чтобы воздействие сдвига закончилось появлением поперечной волны, необходимо, чтобы силе, производящей сдвиг, противостояла другая сила, которая сдвигает части тела обратно, на первоначальные места.