Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 29

Предположим затем, что при вращении вы опускаете руки. Масса ваших рук и грузов, которые они держат, теперь значительно ближе к оси вращения, и, несмотря на то что полная масса не изменилась, момент инерции очень уменьшился. Если момент инерции (I) уменьшился, то угловая скорость со должна быть соответственно увеличена, чтобы угловое количество движения (Iω) оставалось постоянным. (Другими словами, если вам нужно, чтобы произведение двух чисел всегда равнялось 24, а затем изменяете множитель с 8 на 4, то вы должны изменить второй множитель с 3 на 6, чтобы произведение продолжало равняться 24: 24 = 8∙3; 24 = 6∙4; 24 = 4∙6; 24 = 3∙8; 24 = 2∙12…)

Так и получается. Поворотный стол внезапно увеличивает скорость своего вращения, в то время как вы опускаете руки, и также скорость вращения резко уменьшается, когда вы снова поднимаете руки. Фигурист использует этот же принцип при выступлениях на льду: сначала он вращается достаточно быстро с руками раздвинутыми в стороны, а затем руки опускает вниз или вытягивает вертикально вверх и осуществляет стремительное вращение на носке конька.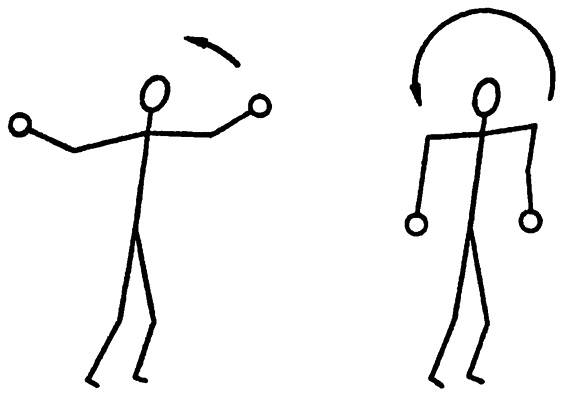

^{Сохранение углового количества движения}

Тело, которое обладает только угловым количеством движения, не может передать неуравновешенное поступательное количество движения к другому телу, поскольку передавать ему нечего. Безусловно, вращающиеся колеса автомобиля дают поступательное количество движения. Но в этом случае, однако, равное по величине, но противоположное по знаку количество движения дает земля. Эти два поступательных импульса складываются, чтобы в результате дать нуль. Любой автомобилист, который когда-либо пробовал двигаться по льду, подтвердит этот факт. Как только трение уменьшилось до величины, когда оно очень малое или никакое количество движения не может быть передано земле, автомобиль получит малое или никакое количество движения, и колеса будут прокручиваться вхолостую.

Законы сохранения нравятся ученым. Во-первых, закон сохранения устанавливает пределы возможностей. При рассмотрении нового явления очень удобно исключить все объяснения, которые повлекли бы нарушение одного из законов сохранения (по крайней мере, пока не придут к выводу, что ничего, за исключением такого нарушения, не может объяснить явление). С оставшимися возможностями тогда гораздо легче работать.

В дополнение ко всему имеется интуитивное чувство, что ничто не возникает из ничего. Поэтому кажется надлежащим и правильным предположить, что Вселенная обладает определенным ограниченным количеством тех или других свойств материи (типа количества движения) и что в то время, как это количество распределено различными способами среди различных тел Вселенной, общая сумма их не может быть ни увеличена, ни уменьшена.

Следовательно, если мы наблюдаем ситуацию, в которой кажется, что в некотором отношении что-то получено из ничего, сразу имеет смысл начать поиск некоторого фактора ситуации, который уменьшается, компенсируя это увеличение. Может оказаться, что это — два фактора, объединенные некоторым способом, которые образуют константу. В случае углового количества движения, например, момент инерции может изменяться по желанию и может, по-видимому, появляться из ниоткуда или исчезать в никуда.

Угловая скорость, однако, всегда сразу изменяется в противоположную сторону, а произведение момента инерции и угловой скорости является константой.

Другой случай такого плана — результат рассмотрения «рычага». Рычаг — это любой твердый объект, способный к вращению вокруг некоторой фиксированной точки, называемой «точкой опоры» рычага. В качестве практического примера можно рассмотреть деревянную доску, лежащую на «козлах»; доска является рычагом, «козлы» — точкой опоры.

Если точка опоры находится точно под центром тяжести рычага, то рычаг останется сбалансированным, то есть не наклонится ни в ту ни в другую сторону. Поскольку рычаг, как и. любой другой объект, ведет себя так, как будто весь его вес сконцентрирован в центре тяжести, он может тогда удержаться целиком на узком крае точки опоры. Если рычаг обладает однородными геометрическими характеристиками и плотностью, центр тяжести его находится в геометрическом центре, и именно туда следует поместить точку опоры, как в известной детской игре — в качелях.

Если к любой точке на рычаге приложить направленную вниз силу, то эта сила, умноженная на расстояние до точки опоры, даст нам крутящий момент и рычаг начнет вращательное движение в направлении крутящего момента.

Предположим, однако, что к рычагу в тоже самое время, во с другой стороны точки опоры прикладывают другую направленную вниз силу. Если вторая сила равна первой и приложена на таком же расстоянии от точки опоры, то полученные два крутящих момента равны по величине, но не по направлению. Крутящий момент на одной стороне точки опоры имеет тенденцию вызывать вращение по часовой стрелке, а тот, что с другой стороны, имеет тенденцию вызывать вращение против часовой стрелки. Если обозначить один крутящий момент как τ, то другой должен быть равен -τ. Эти два крутящих момента складываются, сумма их равна нулю, и рычаг не двигается. Он остается в положении равновесия.

(С другой стороны, если сила приложена вниз на одной стороне точки опоры и вверх на другой, то оба производят движение в том же самом направлении: оба по часовой стрелке или оба против часовой стрелки. Крутящие моменты в этом случае будут одного и того же знака, и сумма их будет составлять 2τ или –2τ. Такой удвоенный крутящий момент называется «парой», и, естественно, пара моментов может более легко переместить рычаг относительно точки опоры. Такую пару мы используем, когда заводим будильник или открываем штопором бутылку.)

Крутящие моменты, используемые при применении рычага, часто образуются под действием грузов, опирающихся на концы балансировочного рычага; они также могут находиться на чашках, установленных на этих концах. Можно сказать, что два равных груза приведут рычаг в положение равновесия, если они помещены на противоположные стороны точки опоры и на равных расстояниях от нее.

Это фактически и является принципом «балансирных весов». Такие весы имеют две чашки равного веса, установленные на концах горизонтального прутка («коромысла», поэтому такие весы также называют «весами с коромыслом». — Пер.), который вращается относительно центральной точки опоры. Если мы поместим объект неизвестного веса в одну чашку, а в другую чашку — набор известных весов (тарированные гирьки) и приведем весы в положение равновесия, то неизвестный вес будет равен сумме известных весов в другой чашке. По этому же принципу мы измеряем массу, а не только вес.

Рычаг, подвергнутый воздействию равных и противоположных по знаку крутящих моментов, считается находящимся «в положении равновесия» («equilibrum» — от латинских слов, означающих «равные веса»). Это выражение применяют к любой системе, находящейся под воздействием сил, которые производят взаимоисключающие эффекты и оставляют общее состояние системы неизменным.