Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 215

С помощью масс-спектрографа Астона (см. гл. 8) удалось с огромной точностью измерить массы отдельных изотопов. Мы знаем, что по отношению к углероду–12 фактическая масса кислорода–18 равна 17,99916, калия–41 — 40,96184, а урана–235 — 23,0439.

Если считать, что ядро состоит из одних лишь нейтронов и протонов, то получились весьма странные результаты. Но разве масса одного нейтрона или протона равна 1? Нет. Относительно углерода–12 масса протона составляет 1,007825, а нейтрона — 1,00865.

Но тогда возникает другой вопрос. Ядро углерода–12 состоит из 6 протонов и 6 нейтронов. Но общая масса 12 отдельно взятых нуклонов равна 12,098940, однако масса тех же самых 12 нуклонов ядра углерода–12 составляет 12,00000, то есть дефект массы равен 0,098940. Куда же делась эта масса?

Понятно, что, согласно формуле Эйнштейна (см. ч. II), избыточная масса перешла в энергию.

При образовании ядра углерода–12 менее 1% общей массы 6 протонов и 6 нейтронов переходит в энергию. Для разложения ядра углерода–12 на отдельные нуклоны требуется энергия, которую накопить достаточно сложно, и именно поэтому ядро углерода–12 не распадается. Энергия, удерживающая нуклоны внутри ядра, гораздо выше энергии, удерживающей атомы внутри молекулы и молекулы внутри твердого вещества. Она также выше энергии, удерживающей электроны внутри атома. Именно поэтому расплавка твердого вещества, разложение химического соединения или даже ионизация атома — плевое дело по сравнению с расщеплением ядра.

И хотя без применения колоссальной энергии расщепить атомное ядро невозможно, внутри его можно провести менее кардинальные изменения, и некоторые из этих изменений происходят спонтанно.

Начнем с того, что чем больше энергии на одну частицу отдается во время формирования ядра путем «упаковки» нескольких отдельных электронов вместе, тем более стабильным будет ядро (при прочих равных). Измерить эту энергию образования ядра можно, выделив массовое число (A) из фактической массы изотопа (A_m). Полученное значение дефекта массы можно разделить на фактическую массу и получить дробное значение дефекта массы. Чтобы избавиться от дроби, результат умножается на 10 000, и в итоге получаем то, что Астон назвал коэффициентом уменьшения массы. Если обозначить его как P_t, то

P_t = 10000(A_m – A)/A_m. (Уравнение 11.1)

Чем меньше коэффициент уменьшения массы, тем больше потери массы при образовании ядра и тем выше его стабильность.

Самый высокий коэффициент уменьшения массы у водорода. Фактическая масса ядра водорода–1 (голого протона) равна 1,007825. Подставив это значение (1,007825) в формулу 11.1 вместо A_m, а 1 — вместо A, коэффициент уменьшения массы получим 78,25, что неудивительно, так как единственный протон при формировании ядра никуда не «упаковывается». У отдельного нейтрона коэффициент уменьшения массы еще больше — 86,7.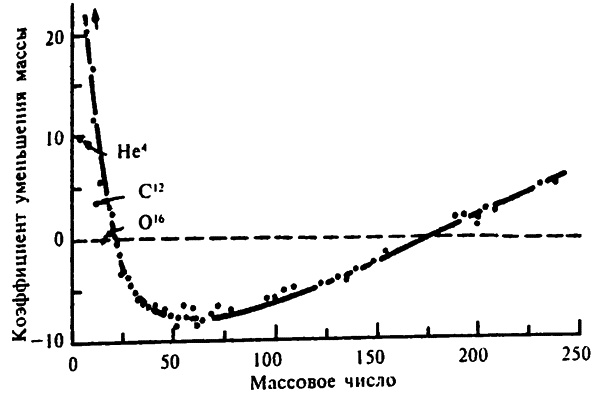

^{Кривая коэффициента уменьшения массы Астона}

С другой стороны, коэффициент уменьшения массы лития–7 равен 22.9. при A_m = 7,01601, а A = 7, в то время как коэффициент уменьшения массы углерода–13 равен 2,4, при A_m — 13,00335,

В целом коэффициент уменьшения массы нескольких следующих за водородом–1 элементов уменьшается. Это говорите том что с усложнением ядра отношение n/p становится более «стабильным». Проще говоря, когда два простых ядра образуют более сложное, выделяется энергия.

Коэффициент уменьшения массы азота–15 равен уже 0, однако у ядер еще более сложных элементов этот коэффициент принимает отрицательные значения. (Как следствие того, что мы приняли атомное число углерода–12 за 12. Если бы мы высчитывали атомные веса относительно того, что атомный вес железа–56 равен 56, то коэффициент уменьшения массы не имел бы отрицательных значений.)

Например, значение A_m калия–41 равно 40,96184 a A = 41, значит, коэффициент уменьшения массы равен) –9,3. Минимальное значение коэффициента уменьшения массы у железа–56 равно –11,63. Затем коэффициент уменьшения массы начинает вновь увеличиваться: например, у олова–120 он равен 8,1, а у иридия–191 равен –2,0. Значения коэффициентов элементов в конце периодической таблицы вновь положительные: коэффициент уменьшения массы урана–238 равен +2,1.

Это значит, что самыми стабильными являются атомы средних размеров, например железа и никеля. Энергия выделяется не распаде более сложных атомов на более простые.

Все это отражено в общем устройстве Вселенной. В целом, согласно проведенному на основе астрономических данных анализу распространенности элементов во Вселенной, оказалось, что чем сложнее элемент, тем реже он встречается. Около 90% всех атомов во Вселенной являются атомами водорода (простейшего элемента) и еще 9% — гелия (второй простейший элемент). Вполне вероятно, что благодаря своей стабильности атомы железа также распространены гораздо больше атомов остальных элементов. На примере нашей планеты можно сказать, что это действительно так: малая масса Земли не позволила ей удержать простейшие атомы, однако по массе она на 35% состоит из атомов железа.

Очень мало значение коэффициента уменьшения массы у атомов углерода–12 и кислорода–16 (которые можно рассматривать как состоящие из альфа-частиц) и особенно мало у атома гелия–4 (который и является альфа-частицей).

Коэффициент уменьшения массы лития–6 равен 25,2, а водорода–2 — 70. Раз гелий–4 находится где-то посредине между этими элементами, то можно предположить, что и его коэффициент уменьшения массы также будет иметь среднее значение коэффициентов этих элементов. Однако коэффициент уменьшения массы гелия–4 всего лишь 6,5, что намного меньше, чем у лития–6 и водорода–2. Неудивительно, что гелий, углерод и кислород — самые распространенные элементы во Вселенной.

Стабильность определенного нуклида зависит от значения не только его собственного коэффициента уменьшения массы, но и коэффициента уменьшения массы нуклидов с таким же количеством нуклонов. Например, сам по себе атом натрия–24 (11 протонов, 13 нейтронов) должен быть стабильным. Однако у атома магния–24 (12 протонов, 12 нейтронов) коэффициент уменьшения массы ниже. Поэтому, испуская бета-частицу и меняя тем самым соотношение нуклонов с 11–13 до 12–12, атом магния–24 становится стабильным. В то время как для полного разложения ядра натрия–24 необходимы гигантские энергетические затраты, лишь небольшое количество энергии достаточно для преобразования ядра путем испускания бета-частицы. Атом натрия–24 самопроизвольно испускает бета-частицу и распадется до атома магния–24, период полураспада которого составляет 15 часов.

Сразу два соседних изотопа с равными значениями массового числа не могут быть стабильными. Изотоп с большим коэффициентом уменьшения массы самопроизвольно преобразуется в изотоп с меньшим коэффициентом. Это все равно что скатиться с «энергетической горки»: чем круче горка, тем меньше период полураспада.