Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 20

Взаимодействующие силы на полюсах равны нулю и плавно возрастают при приближении к экватору. Одновременно возрастает и «растяжение» земной поверхности, которое достигает своего максимального значения на экваторе. Из-за этой экваториальной выпуклости расстояние от центра Земли до уровня моря на экваторе на 21 км (13 миль) больше, чем такое же расстояние на любом из полюсов.

Земля поэтому не сфера, а сплющенный сфероид.

Безусловно, 21 км при полном расстоянии в 6370 км — это немного, но и этого вполне достаточно, чтобы внести существенные различия в значение g. Что же касается выпуклости на экваторе и локальных различий в высоте, то, например, в штате Аляска есть точки, где значение g больше чем 9,82 м/с², в то время как на экваторе это значение — только чуть выше, чем 9,78 м/с². Представленные цифры отражают разницу в почти полпроцента и соответственно отражаются на весе.

Другими словами, вес объекта в значительной мере изменяется при перемещении его с места на место по поверхности Земли, что и показывают пружинные весы. Человек, который весит 200 фунтов на полюсах, весил бы 199 фунтов на экваторе. Химику или физику, заинтересованному в массе объекта (многие свойства объектов зависят от массы), такое «замещение» измерения массы измерением веса доставило бы серьезные погрешности.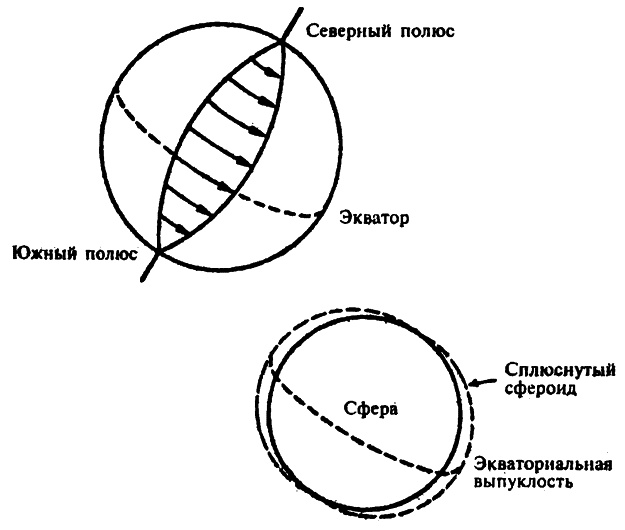

^{Центробежная сила и экваториальная выпуклость}

Ученые обычно, когда у них возникает необходимость «взвесить» объект, используют весы, состоящие из двух чашек, расположенных на противоположных концах прутка, который в середине установлен на шарнире. В одну чашку помещают объекты известного веса, а в другую — объект, который необходимо взвесить. Известные веса добавляют до тех пор, пока вся конструкция не сбалансируется. В этом случае сила тяжести на обеих чашках становится одинаковой (если бы она была большей на любой из них, то эта чашка опустилась бы, в то время как другая поднялась бы вверх).

Если вес с обеих сторон один и тот же, то и mg будет с обеих сторон одинаковым, так как g, которое в больших пределах изменяется в зависимости от точки земной поверхности, на которой находится тело, будет одно и то же для двух чашек весов, стоящих рядом на практически одной и той же точке земной поверхности. Поэтому масса m объектов, находящихся в обеих чашах весов, будет одна и та же. То есть масса неизвестного объекта будет равна массе грузов (вес которых нам известен) ^[20].

Естественно, мелкие изменения в значениях g становятся все большими по мере удаления тела от центра Земли. Дальнейшее усложнение ситуации представляет собой то, что при удалении тела на большое расстояние от Земли мы можем приблизить его к некоторому другому значительному скоплению массы. Такая ситуация возникает в первую очередь в связи с Луной и имеет очень важное значение, поскольку искусственные объекты уже приземлились там, а живые люди могут встать на поверхность Луны в ближайшие несколько лет ^[21].

Объект на поверхности Луны все еще находится в пределах поля тяготения Земли, которое простирается не только на Луну, но и в принципе на всю Вселенную. Однако Луна также имеет собственное поле тяготения. Это поле намного слабее, чем земное, поскольку Луна намного менее массивна, чем Земля, а объект на поверхности Луны находится намного ближе к центру Луны, чем к центру Земли; гравитационное притяжение Луны поэтому гораздо сильнее, чем таковое у отдаленной Земли, и человек, стоящий на поверхности Луны, будет ощущать только ее притяжение.

Но Луна притягивает к своей поверхности объект отнюдь не с той же силой, как это делает Земля. Чтобы увидеть разницу между этими двумя силами, обратимся назад, к уравнению 4.1, которое утверждает, что F = Gmm’/d². Эта F представляет собой интенсивность притяжения Земли, с которым она воздействует на объект на ее поверхности. Притяжение Луны, с которым она воздействует на объект на ее поверхности, мы можем обозначить F_m.

Далее, объект имеет одну и ту же массу независимо от того, находится ли он на поверхности Земли или на поверхности Луны, так что m остается неизменным. Значение G также неизменно, поскольку оно является константой повсюду во Вселенной. Масса Луны, однако, как известно, является ¹/₈₁ массы (m’) Земли. Масса Луны, следовательно, равна m’/81. Расстояние от поверхности Луны до ее центра — 1737 км, или примерно ³/₁₁, расстояния от поверхности Земли до ее центра, равного 6370 км (d). Следовательно, мы можем выразить расстояние от поверхности Луны до ее центра как 3d/11.

Теперь подставим эти значения в уравнение 4.1, используя массу и радиус Луны, и мы получим уравнение, которое выражает значение силы притяжения Луны для объекта, находящегося на ее поверхности. Итак, это:

Fm = Gm(m’/81)/(3d/11)² (Уравнение 5.3)

Если мы теперь разделим уравнение 5.3 на уравнение 4.1, то найдем, что F_m/F) (отношение силы тяжести на Луне к силе тяжести на Земле) равно ¹/₈₁, разделенной на (³/₁₁)², или почти точно — ¹/₆. Таким образом, сила тяжести, которую мы испытали бы на поверхности Луны, будет равна ¹/₆ той, к которой мы привыкли на поверхности Земли. Человек весом в 180 фунтов, взвесив себя на пружинных весах, найдет, что он весит всего 30 фунтов.

Но, несмотря на столь решительное уменьшение веса, масса объекта останется неизменной. Это означает, что сила, требующаяся, чтобы ускорить данный объект до данной величины, остается той же самой и на Луне, и на Земле. Мы могли бы поднять в воздух своего 180-фунтового друга без особых усилий, поскольку усилие подъема будет не больше, чем то, которое мы развиваем на Земле, поднимая 30 фунтов. Однако на Луне мы не могли бы поднять человека более быстро, чем на Земле. Здесь, на Земле, мы можем достаточно легко управиться с чем-то, что весит 30 фунтов. Но на Луне это что-то, весящее 30 фунтов, будет иметь массу в шесть раз больше «нормальной», а такое количество массы можно переместить только достаточно медленно. По этой причине манипулирование объектами на поверхности Луны создает чувство «замедленного движения», или как будто проталкиваешься сквозь патоку.

Опять же, если мы подпрыгиваем на Луне, силе наших мускулов будет противостоять только ¹/₆ той силы тяготения, к которой мы привыкли на Земле. Поэтому центр нашего тела поднимется на высоту в шесть раз большую, чем это было бы на Земле. Достигнув этой необычной высоты, мы будем падать по направлению к поверхности, но с ускорением, составляющим ¹/₆ обычного ускорения (1,63 м/с²). Это означает, что мы, внешне, как бы падали медленно вниз, «планируя, подобно перу». Однако к тому времени, когда бы мы снова достигли поверхности с ¹/₆ от обычного ускорения и с расстояния большего в шесть раз, мы к моменту приземления все равно бы достигли той скорости, с которой мы приземлились бы после прыжка на Земле (затратив для этого равное усилие, но достигнув значительно меньшей высоты).