Популярная физика. От архимедова рычага до квантовой теории - читать онлайн книгу. Автор: Айзек Азимов cтр.№ 132

Сила же между магнитными полюсами изменяется в зависимости от природы находящейся между ними среды, и уравнение 9.1 точно соблюдается только тогда, когда между полюсами вакуум. Чтобы объяснить это, надо узнать об исследованиях английского ученого Майкла Фарадея (1791–1867).

В 1831 году он заметил нечто, что было замечено на пять веков раньше Петером Перегринусом и, несомненно, еще множеством людей, игравших с магнитами на протяжении веков… Начнем с того, что поместим лист бумаги на магнитную полоску. Если на бумагу насыпать железные опилки и потрясти ее, опилки начнут двигаться и располагаться по линиям, изгибающимся от одного полюса магнита до другого. Каждая линия начинается на одном полюсе и заканчивается на другом, пересекающихся среди них не будет. (Конечно, некоторые линии окажутся незамкнутыми, потому что они выходят за лист бумаги или потому что на больших расстояниях от полюсов их влияние слишком слабо, чтоб заставить железные опилки строго следовать линиям. Все равно можно предположить, что все линии, как бы далеко они ни уходили и какими бы слабыми ни становились, являются непрерывными от полюса к полюсу.)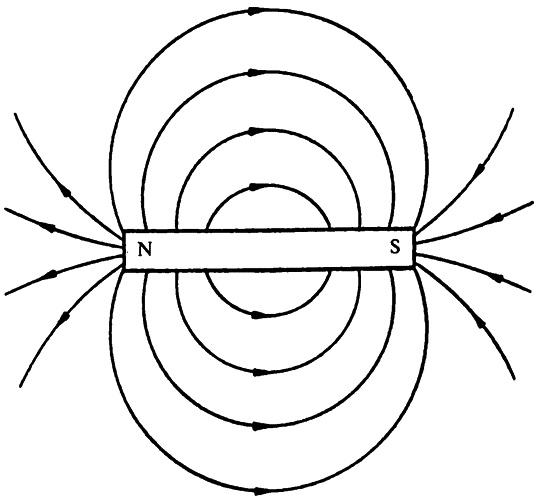

^{Магнитные силовые линии}

Форма этих линий зависит от формы магнита и взаимоотношений полюсов. В случае подковообразного магнита линии, собирающиеся около двух полюсов и в пространстве между ними, прямые. То же самое, если северный полюс одного магнитного бруска поднести к южному полюсу другого. С другой стороны, если северный полюс одного бруска поднести к северному полюсу другого, то силовые линии изогнутся наружу в стремлении линий одного магнита избежать линий другого.

Фарадей назвал их силовыми магнитными линиями и полагал, что они реально существуют. Он считал, что они сделаны из некоего гибкого материала, который растягивается, когда распространяется между двумя различными полюсами, что высвобождает силу, необходимую для его сокращения обратно, как это произошло бы с растянутым резиновым жгутом. И именно это стремление к сокращению и порождает магнитное притяжение, решил Фарадей.

Силовые линии вокруг магнита любой формы или вокруг любой системы магнитов можно визуализировать и без железных опилок. Стрелка компаса всегда располагается так, чтобы лежать вдоль одной из этих линий. Следовательно, выясняя направление стрелки компаса в различных точках пространства, можно выяснить расположение этих линий. Таким образом можно определить и силовые линии Земли как магнита.

Представление Фарадея о материальном присутствии силовых линий просуществовало недолго. К середине XIX века в связи с вопросом о природе света сильные позиции приобрела концепция эфира (см. гл. 6), и силовые магнитные линии стали считать искажением эфира.

С исчезновением в начале XX века концепции эфира нужно было предпринимать дальнейшие шаги. Снова это стало вопросом геометрии самого пространства. Предположим, например, что вы уронили карандаш в цилиндрическое отверстие. Он автоматически сориентируется параллельно оси цилиндра. Если бы цилиндр оказался растянувшейся на многие мили трубой, слегка изгибающейся туда-сюда, упавший карандаш продолжал бы в любой точке ориентироваться параллельно оси трубы, каким бы ни было в данном месте ее направление.

Фактически, если вы не можете увидеть саму трубу, а только карандаш, вы легко можете разметить ее искривления по положениям, которые принимает в различных точках карандаш. То же верно и для стрелки компаса, и для магнитных силовых линий.

Каждый магнитный полюс воздействует на геометрию всего пространства, и эта измененная геометрия (по сравнению с геометрией, какой она была бы в отсутствие магнитного полюса) называется магнитным полем. Интенсивность этого магнитного поля (насколько его геометрия отличается от обычной немагнитной геометрии пространства) падает пропорционально квадрату расстояния до полюса и вскоре становится слишком маленькой, чтобы ее можно было различить.

Тем не менее магнитное поле каждого существующего магнитного полюса наполняет все пространство, и ситуация становится терпимой только потому, что воздействие любого полюса, находящегося рядом, перевешивает все остальные настолько, что его действие можно считать изолированным (к гравитационным полям это тоже относится).

Представление о магнитном поле устраняет необходимость предполагать, что магнитная сила — это воздействие на расстоянии. Магнит не притягивает железо на расстоянии, а создает поле, которое влияет на кусок железа внутри себя. Поле (представляющее собой геометрию пространства) касается и магнита, и железа, и никакого воздействия на расстоянии предполагать не требуется.

Несмотря на то что магнитные силовые линии не существуют материально, часто бывает удобно нарисовать их в буквальном смысле и использовать для объяснения поведения предметов в магнитном поле. (Делая так, мы используем «модель», то есть представление о Вселенной, не являющееся реальным, но помогающее рассуждать. Ученые используют множество моделей, и они чрезвычайно полезны. Опасность заключается в том, что всегда появляются попытки утверждать реальность моделей, чтобы их можно было использовать за пределами их действия. Может возникнуть и неосознанное сопротивление любым изменениям, которые приносит новое знание, если их нельзя уложить в эту модель.)

Мы можем определить силовые линии между двумя магнитными полюсами в системе СГС (используя сантиметры и дины) таким образом, что одна линия силы будет установлена в 1 максвелл (в честь Максвелла, который так много сделал в связи как с газами, так и со светом). В системе МКС, где те же измерения производятся в метрах и ньютонах, линия силы устанавливается в 1 вебер (в честь немецкого физика Вильгельма Эдуарда Вебера (1804–1891). Вебер — гораздо большая единица, 1 вебер равен 100 000 000 максвеллов. Максвеллы и веберы — единицы измерения магнитного потока, которое можно представить как количество силовых линий, проходящих через данную область, перпендикулярную этим линиям.

Измеряя силу магнитного поля, нужно сосчитать количество силовых линий, проходящих через область определенного размера. Это плотность магнитного потока.

Плотность потока показывает, насколько близко друг к другу проходят силовые линии; чем они более кучны, тем выше плотность потока и тем сильнее магнитное поле в этой точке. В системе СГС единица площади — квадратный сантиметр, так что единица измерения плотности потока — 1 максвелл на квадратный сантиметр. Она получила название 1 гаусс в честь немецкого математика Карла Фридриха Гаусса (1777–1855) ^[97]. В системе МКС единица измерения площади — квадратный метр, следовательно, единица измерения магнитного потока — 1 вебер на квадратный метр, у этой единицы нет специального названия. Поскольку в квадратном метре 10 000 квадратных сантиметров, а в вебере 100 000 000 максвеллов, то 1 вебер на квадратный сантиметр равен 10 000 гауссов.