Число Бога. Золотое сечение – формула мироздания - читать онлайн книгу. Автор: Марио Ливио cтр.№ 59

Так вот, интересный вопрос: почему эти два выдающихся космолога решили побаловаться занимательной математикой – и перешли к квазикристаллам?

Я знаком с Пенроузом и Стейнхардтом уже много лет, поскольку занимаюсь тем же делом – космологией и теоретической астрофизикой. Более того, в 1984 году Пенроуз получил приглашение выступить на первой крупной конференции по релятивистской астрофизике, которую я организовывал, а Стейнхардт – на последней, в 2001 году. И тем не менее, я не знал, что подтолкнуло их к тому, чтобы углубиться в дебри занимательной математики: казалось бы, эта область довольно далека от их профессиональных интересов в астрофизике. Поэтому я спросил у них об этом.

Роджер Пенроуз ответил:

– Не уверен, что дам на этот вопрос сколько-нибудь глубокий ответ. Как вам известно, математика – занятие, которому большинство математиков предается ради удовольствия. – И, немного поразмыслив, добавил: – Я с детства любил подгонять геометрические фигуры друг к другу, так что исследования мозаик опередили исследования по космологии. Однако в какой-то момент изыскания в области занимательной математики были, по крайней мере, отчасти, связаны с космологическими исследованиями. Я размышлял о крупномасштабной структуре Вселенной и искал игрушечные модели, построенные по простым правилам, которые, тем не менее в крупном масштабе были бы способны породить сложные структуры.

– Но что же заставило вас так долго работать над этой задачей? – спросил я тогда.

– Как вы знаете, меня всегда интересовала геометрия, – со смехом ответил Пенроуз, – так что мне было просто интересно разобраться в этой задаче. Более того, хотя у меня было подозрение, что подобные структуры могут встречаться в природе, я не понимал, как природа могла бы создать их посредством нормального процесса кристаллического роста, локального процесса. В некотором смысле я до сих пор этого не понимаю.

А Пол Стейнхардт на мой вопрос по телефону тут же воскликнул:

– Хороший вопрос!

А затем, подумав несколько минут, рассказал:

– Когда я был студентом-старшекурсником, то не вполне представлял себе, чем хочу заниматься. Затем, уже в аспирантуре, я день и ночь ломал себе голову над физикой частиц, и мне нужно было найти какую-то отдушину – вот и я стал для развлечения исследовать тему порядка и симметрии твердых тел. А стоило мне натолкнуться на проблему квазипериодических кристаллов, как я понял, что это непреодолимое искушение, и с тех пор то и дело возвращался к ней.

Модель квазикристаллов Стейнхардта-Джуна обладает одним интересным свойством: она создает дальний порядок из взаимодействий соседних элементов, однако полностью периодический кристалл при этом не получается. Невероятно, но факт: в общем и целом это же свойство мы обнаруживаем у чисел Фибоначчи. Рассмотрим простой алгоритм, позволяющий создать последовательность, получившую название золотой последовательности. Начнем с числа 1, затем заменим 1 на 10. Теперь будем заменять все 1 на 10, а все 0 на 1. Тогда у нас получатся следующие этапы:

1

10

101

10110

10110101

1011010110110

101101011011010110101

И так далее. Очевидно, что мы начали с «ближнего» правила (простое превращение 0 в 1 и 1 в 10), а получили непериодический «дальний порядок». Обратите внимание, что количество цифр 1 в каждой строчке составляет 1, 1, 2, 3, 5, 8. ., то есть числа Фибоначчи, как и количество цифр 0, начиная со второй строчки. Более того, отношение числа единиц к числу 0 по мере удлинения последовательности становится все ближе к φ. Далее, изучение рис. 27 показывает, что если обозначить новорожденную пару крольчат 0, а взрослую пару 1, то количество пар кроликов будет в точности повторять только что приведенную последовательность. Однако неожиданные свойства золотой последовательности этим не исчерпываются. Если начать с 1 (в первой строчке), за которым следует 10 (вторая строчка) и попросту приписывать к каждой строчке непосредственно предшествующую, тоже получится цельная последовательность. То есть четвертая строчка 10110 получается, если приписать вторую – 10 – к третьей – 101, и т. д.

Вспомним, что самоподобие означает симметрию при любом масштабе. Логарифмическая спираль обладает самоподобием, поскольку, как ее ни увеличивай, выглядит всегда одинаково, как и череда вписанных друг в друга правильных пятиугольников и пентаграмм на рис. 10. Каждый раз, когда вы приходите в парикмахерскую, вы видите бесконечную череду собственных самоподобных отражений в двух параллельных зеркалах.

Так вот, золотая последовательность тоже самоподобна при любом масштабе. Возьмем последовательность

1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1…

И посмотрим на нее в лупу – конечно, не в буквальном смысле слова. Начнем слева и каждый раз, когда нам встретится 1, будем помечать группу из трех символов, а когда нам встретится 0 – группу из двух символов, только так, чтобы группы не перекрывались. Например, первая цифра у нас 1, поэтому мы отметим группу из первых трех символов – 101 (см. ниже). Вторая цифра в ряду у нас 0, поэтому мы отметим группу из двух символов 10, следующую за первой группой 101. Третья цифра – 1, значит, отмечаем три цифры 101, которые следуют за 10, и т. д. Теперь размеченная последовательность выглядит так: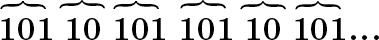

101 10 101 101 10 101…

А теперь оставим первые две цифры из каждой группы по три и первую – из каждой группы по две (то, что мы оставляем, подчеркнуто):

И взглянем на получившуюся последовательность из оставшихся цифр:

1 0 1 1 0 1 0 1 1 0…

Как видите, она идентична золотой последовательности.

Можно проделать и другое упражнение по увеличению золотой последовательности путем подчеркивания той или иной закономерной подпоследовательности. Скажем, в качестве подпоследовательности выберем 10 и будем подчеркивать это сочетание цифр в золотой последовательности везде, где оно встретится: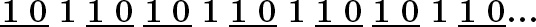

Если теперь мы будем обращаться с каждым сочетанием 10 как с единым символом и обозначим количество мест, на которые надо сдвинуть каждое сочетание 10, чтобы перекрыть его со следующим 10, то получим последовательность 2122121… (первое 10 надо сдвинуть на два места, чтобы оно наложилось на следующее, третье – на одно место и так далее). Если теперь в получившейся последовательности заменить каждую цифру 2 цифрой 1 и каждую 1 – нулем, мы снова получим золотую последовательность. В общем, если взять любую закономерность в пределах золотой последовательности, мы обнаружим, что та же закономерность присутствует в последовательности и при ином масштабе.