Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса - читать онлайн книгу. Автор: Марио Ливио cтр.№ 62

Последующие сорок лет математики провели в исследованиях системы понятий для многочлена Александера и тщательном изучении свойств узлов. Почему же они так углубились в эту область? Очевидно, не ради какой-то практической пользы. Модель атома Томсона была уже давно позабыта, а другой задачи, которая требовала бы решения на основе теории узлов, в поле зрения не наблюдалось – ни в естественных науках, ни в экономике, ни в архитектуре, ни в других дисциплинах. Математики тратили бесконечные часы на изучение узлов из чистого любопытства! Для них идея узлов и принципы, которые ими управляют, обладали изысканной красотой. Внезапное озарение, полученное благодаря многочлену Александера, было для математиков таким же непреодолимым искушением, как и задача покорить гору Эверест для Джорджа Мэллори, который, как известно, на вопрос, почему ему так хочется взобраться на эту гору, ответил: «Да потому что она есть!».

В конце 1960-х годов плодовитый англо-американский математик Джон Хортон Конвэй описал процедуру постепенного «развязывания» узлов и тем самым вскрыл глубинные отношения между узлами и их многочленами Александера (Conway 1970). В частности, Конвей предложил две простые «хирургические» операции, которые могли послужить основой для определения инварианта узла. Операции Конвея, получившие названия флип и сглаживание, схематически изображены на рис. 56. При флипе (рис. 56, а) для трансформации пересечения верхний участок струны пропускают под нижним (на рисунке также видно, как проделать эту трансформацию с настоящим узлом на веревке). Обратите внимание, что флип, очевидно, меняет самую природу узла. Например, легко убедиться, что узел-трилистник с рис. 54, b в результате флипа станет незаузленным узлом (рис. 54, а). Операция сглаживания по Конвею вовсе убирает пересечение (рис. 56, b) – для этого нужно «разрезать» струну и «склеить» не те концы.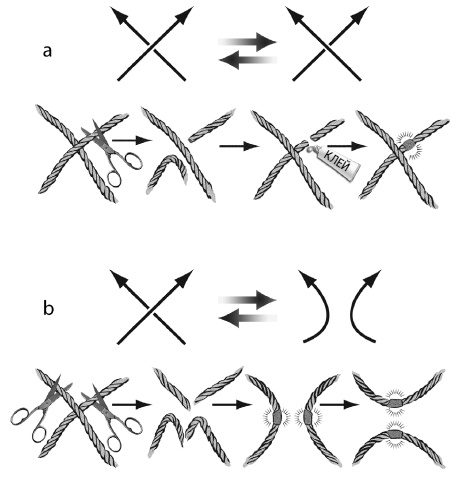

Рис. 56

Благодаря трудам Конвея математики стали по-новому понимать устройство узлов, но все же еще лет двадцать были уверены, что других инвариантов узлов (наподобие многочлена Александера) уже не найдется. Однако в 1984 году положение дел резко изменилось.

Новозеландско-американский математик Вон Джонс вообще не изучал узлы. Он исследовал мир еще более абстрактный – так называемые алгебры фон Неймана. И неожиданно для себя обнаружил, что в алгебрах фон Неймана есть некое соотношение, подозрительно похожее на одно соотношение из теории узлов. Тогда Джонс встретился с Джоан Бирман, специалистом по теории узлов из Колумбийского университета, чтобы обсудить, что с этим можно сделать. Изучение этого соотношения в результате выявило совершенно новый инвариант узлов – так называемый многочлен Джонса (Jones 1985). Математики сразу признали, что многочлен Джонса – куда более тонкий инвариант, чем многочлен Александера. В частности, он позволяет отличать узел от его зеркального отражения (то есть «левый» трилистник на рис. 57 от «правого»), а многочлены Александера для таких узлов тождественны. Однако главное даже не это, а то, что открытие Джонса вызвало у специалистов по теории узлов небывалый прилив энтузиазма. Когда было объявлено об открытии нового инварианта, в мире узлов внезапно вспыхнула бешеная активность, прямо как на фондовой бирже в день, когда Федеральная резервная система ни с того ни с сего понижает процентные ставки.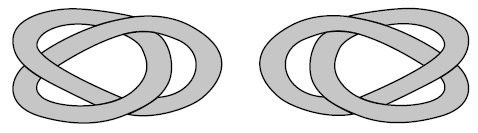

Рис. 57

Однако, невзирая на то, что за прошедшие три десятилетия были обнаружены и другие инварианты, пока не удается составить полную классификацию узлов. Вопрос о том, какой именно узел можно превратить в другой узел, если вертеть его и крутить, не прибегая к помощи ножниц, остается без ответа. Пока что самый удачный инвариант – это творение русско-французского математика Максима Концевича, который получил за него Филдсовскую медаль в 1998 году и Премию Крафорда в 2008 году. Кстати, в 1998 году Джим Хосте из Колледжа Питцера в Клермонте в штате Калифорния и Джеффри Уикс из Кантона в штате Нью-Йорк составили таблицу всех узлов до шестнадцати пересечений включительно. Точно такую же таблицу независимо от них составил Морвен Тистлетвейт из Университета штата Теннесси в Ноксвилле. В каждой из этих таблиц содержится ровно 1 701 936 разных узлов!

Но главная неожиданность таилась не столько в прогрессе теории узлов как таковой, а в том, какой мощный и внезапный толчок она дала самым разным не связанным с ней наукам ^[149].

Стимулом для создания теории узлов была ошибочная модель атома, однако кончина этой модели не обескуражила математиков. Напротив, они с превеликим энтузиазмом пустились в далекий и опасный путь и стали разбираться в узлах как таковых. Легко представить себе, в какой восторг они пришли, когда теория узлов вдруг оказалась ключом к пониманию фундаментальных процессов, в которых участвуют молекулы жизни. Неужели вам мало такого замечательного примера «пассивной» роли чистой математики в объяснении природных явлений?

Дезоксирибонуклеиновая кислота, она же ДНК, – это генетический материал всех клеток на свете. Она состоит из двух очень длинных цепочек, которые миллионы раз перекручены, так что получается двойная спираль. По всей длине этих цепочек, которые можно представить себе как боковины лестницы, чередуются молекулы сахара и фосфата. Ступеньки этой лестницы состоят из пар оснований, соединенных водородными связями по определенным правилам (аденин создает связи только с тимином, а цитозин – только с гуанином; рис. 58).

Когда клетка делится, первым делом начинается самовоспроизведение – репликация ДНК, чтобы каждой из дочерних клеток досталось по копии. Подобным же образом в процессе транскрипции, при которой генетическая информация из ДНК копируется в РНК, участок двойной спирали ДНК раскручивается, и образцом для копирования служит только одна из двух цепочек. После завершения синтеза РНК цепочки ДНК снова скручиваются в спираль. Однако и репликация, и транскрипция – дело непростое, поскольку ДНК так туго скручена и перепутана (информацию нужно хранить в компактном виде), что без особых технологий распаковки процессы, лежащие в основе самой жизни, не могли бы идти гладко. Кроме того, чтобы процесс репликации дошел до конца, получившиеся молекулы ДНК должны быть без узлов, а родительская ДНК в конце концов должна вернуться к первоначальной конфигурации.