Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса - читать онлайн книгу. Автор: Марио Ливио cтр.№ 28

Когда на человека вешают ярлык «современный», то обычно имеют в виду, что он из тех, кто способен спокойно общаться со своими собратьями по профессии, живущими в ХХ, а теперь уже и в XXI веке. Подлинно современным человеком Декарта делает то, что он осмелился подвергнуть сомнению все философские и научные утверждения, сделанные до него ^[58]. Как-то раз он отметил, что образование лишь усилило его растерянность и заставило осознать собственное невежество. В своем прославленном «Рассуждении о методе» Декарт писал: «О философии скажу одно: …в течение многих веков она разрабатывается превосходнейшими умами и, несмотря на это, в ней доныне нет положения, которое не служило бы предметом споров и, следовательно, не было бы сомнительным (здесь и далее цитаты из “Рассуждения о методе” даны в пер. Г. Слюсарева и А. Юшкевича)». Хотя судьба многих философских идей самого Декарта свидетельствует о таких же существенных недочетах в его предпосылках, на которые указывали более поздние философы, освежающий скептицизм, с которым он относился даже к самым основным понятиям, делает его, конечно, современным до мозга костей. Однако главное для нашей книги даже не это: Декарт понимал, что методы и процесс рассуждений в математике приводит именно к той определенности, которой так не хватало схоластической философии прежних времен ^[59]. Он недвусмысленно провозглашал следующее:

В некотором смысле это смелое заявление идет даже дальше воззрений Галилея. Не только физическая Вселенная написана на языке математики – логике математики следует все человеческое знание. По словам Декарта: «Я убежден, что она [математика] превосходит любое другое знание, переданное нам людьми, так как она служит источником всех других знаний» (Пер. М. Гранцева). Поэтому одной из целей Декарта стало продемонстрировать, что мир физики, который для него был реальностью, подлежащей математическому описанию, можно изобразить, не полагаясь на чувственное восприятие, которое так часто нас подводит. Он настаивает, что разум должен тщательно просеивать все то, что видит глаз, и обращать восприятие в идеи. В конце концов, утверждал Декарт, «сон никогда не может быть отличен от бодрствования с помощью верных признаков» (Здесь и далее цитаты из «Размышлений о первой философии» даны в переводе С. Шейнман-Топштейн). Однако Декарт задавался и таким вопросом: если все, что мы воспринимаем как реальность, на самом деле только сон, откуда мы знаем, что и Земля, и небо – не своего рода «сонный обман», который наслал на наши чувства некий «злобный демон, наделенный беспредельным могуществом»? Или, как выразился однажды Вуди Аллен: «Вдруг все лишь иллюзия и ничего на самом деле не существует? В таком случае я, конечно, переплатил за ковер».

Этот шквал болезненных сомнений и привел Декарта к формулировке его самого знаменитого принципа: «Cogito ergo sum» – «Я мыслю, следовательно, существую» ^[60]. Иначе говоря, за любыми мыслями обязательно стоит сознание. Как ни парадоксально, в самом акте сомнений сомневаться нельзя! На этом довольно шатком основании Декарт попытался построить полный алгоритм поиска надежных знаний. Декарт вплотную занимался всем, что его интересовало, – философией, оптикой, механикой, медициной, эмбриологией, метеорологией – и везде оставил свой значительный след. И все же, несмотря на убежденность в способности человека строить причинно-следственные связи, Декарт не считал, что фундаментальные открытия можно совершать при помощи одной лишь логики. В сущности, он пришел к тому же выводу, что и Галилей: «Я заметил, что в логике ее силлогизмы и большинство других правил служат больше для объяснения другим того, что нам известно, или… учат тому, чтобы говорить, не задумываясь о том, чего не знаешь, вместо того чтобы познавать это». Декарт пошел другим путем и, поставив перед собой поистине героическую цель заново изобрести или заложить основы целых научных дисциплин, попытался применить принципы, которые он получил при помощи математического метода, чтобы точно знать, что он на верном пути. Эти строгие законы он описал в своих «Правилах для руководства ума». Начинать надо с истин, в которых нет никаких сомнений (подобно аксиомам в евклидовой геометрии), трудные задачи следует разбивать на более простые, переходить от зачаточного к сложному и дважды проверять всю процедуру, дабы убедиться, что не было упущено ни одного возможного решения. Нет нужды говорить, что даже столь тщательно выстроенный и строгий процесс не обеспечил выводам Декарта полную безошибочность. Более того, хотя Декарт прославился в основном колоссальными прорывами в философии, именно его достижения в математике сохраняют актуальность и по сей день. Расскажу об одной его идее, простой, как все гениальное. Это ее Джон Стюарт Милл назвал «величайшим шагом, сделанным в прогрессе точных наук за всю их историю».

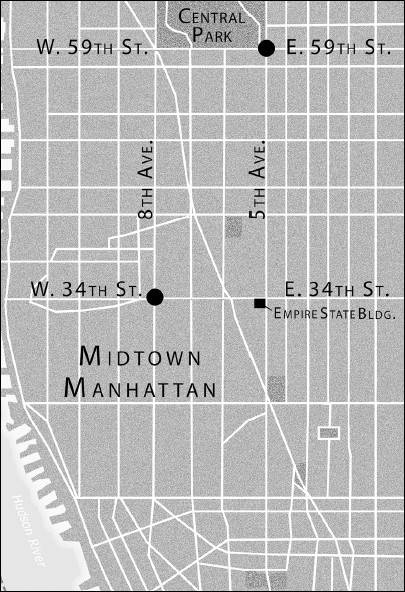
Рис. 24

Взгляните на фрагмент карты Манхэттена на рис. 24. Если вы стоите на углу Тридцать четвертой улицы и Восьмой авеню, а у вас назначено свидание на углу Пятьдесят девятой улицы и Пятой авеню, найти дорогу не составит труда, верно? Именно в этом и заключалась идея новой геометрии по Декарту. Он снабдил свое «Рассуждение о методе» приложением «Геометрия» объемом в 106 страниц ^[61]. Трудно поверить, что эта поразительно простая концепция совершила настоящую революцию в математике. Начал Декарт с почти что тривиального факта: как показывает карта Манхэттена, пара чисел однозначно определяет положение точки на плоскости (например, точка А на рис. 25, а). Затем, опираясь на этот факт, Декарт разработал мощную теорию кривых – аналитическую геометрию. В честь Декарта пара перпендикулярных прямых, которая дает нам систему отсчета, получила название «Декартова система координат». По традиции горизонтальную линию называют «ось х», вертикальную – «ось у», а точку их пересечения – «начало координат». Например, точка, обозначенная А на рис. 25, а, имеет координаты х = 3 и у = 5, что принято обозначать упорядоченной парой чисел (3, 5) (обратите внимание, что начало координат обозначается (0, 0)). А теперь предположим, что мы хотим как-то охарактеризовать все точки на плоскости, которые находятся на расстоянии ровно 5 единиц от начала координат. Разумеется, это и есть геометрическое определение окружности с центром в начале координат и с радиусом в 5 единиц (рис. 25, b). Если вы возьмете точку (3, 4) на этой окружности, то окажется, что ее координаты удовлетворяют равенству 3² + 4² = 52. Более того, легко показать (при помощи теоремы Пифагора), что координаты (x, y) любой точки этой окружности удовлетворяют равенству х ² + у ² = 5². Но и этого мало: точки на окружности – это единственные точки на плоскости, для которых верно уравнение х ² + у² = 5². Это значит, что алгебраическое уравнение х ² + у² = 5² характеризует окружность точно и однозначно. Иначе говоря, Декарт открыл ^[62] способ выразить геометрическую кривую алгебраическим уравнением или численно – и наоборот. Наверное, когда речь идет просто об окружности, кажется, будто в этом нет ничего особенно интересного, однако все на свете графики – будь то недельные колебания фондовой биржи, температура на Северном полюсе за последние сто лет или темп расширения Вселенной – основаны на гениальной идее Декарта. Алгебра и геометрия внезапно перестали быть двумя независимыми отраслями математики и превратились в два представления одних и тех же истин. Уравнение, описывающее кривую, неявно содержит все мыслимые свойства этой кривой, в том числе, например, все теоремы евклидовой геометрии. Но и это еще не все. Декарт показал, что если начертить в одной и той же системе координат разные кривые, то точки их пересечения задаются общими решениями соответствующих алгебраических уравнений. Таким образом Декарт сумел задействовать мощности алгебры, чтобы исправить неприятные недостатки классической геометрии. Например, Евклид определял точку как сущность, не имеющую ни частей, ни величины. Это довольно темное определение навсегда кануло в забвение, когда Декарт определил точку на плоскости просто как упорядоченную пару чисел (x, y). Но даже эти открытия – всего лишь верхушка айсберга. Если две переменные величины x и y можно соотнести таким образом, чтобы каждому значению х соответствовало одно и только одно значение у, они составляют так называемую функцию, а функции воистину вездесущи. Когда вы отслеживаете уменьшение веса во время диеты, рост вашего ребенка в дни рождения или зависимость расхода топлива от скорости вождения, все эти данные можно выразить в виде функций.