Игра случая. Математика и мифология совпадения - читать онлайн книгу. Автор: Джозеф Мазур cтр.№ 27

Предположим, что она знакомится с N > 770 отдельных людей за 5 лет и в некоем подмножестве этого N случайных встреч в разговоре касаются темы дня рождения. Проблема решения всей задачи не в том, что только у одного из 770 может быть та же дата рождения, а в том, что она неумышленно узнала об этом в ходе разговора, когда речь случайно зашла о днях рождения. Каковы шансы этого? Сложность в том, чтобы оценить, насколько часто она заводит разговор о днях рождения. Положим, что в среднем за период в 10 лет в одном из 100 разговоров она касается темы дня рождения. Тогда мы должны умножить число новых знакомых на 100. Другими словами, чтобы иметь 10 %-ный шанс узнать, что один из ее знакомых родился в тот же день, что и она, ей потребовалось бы 77 000 новых встреч. Чтобы иметь шанс встретить такого человека выше 1 к 1, потребуется 510 500 встреч. Но Агнесс утверждает, что с ней это случилось дважды! Кроме того, это были не просто рабочие встречи, а скорее, торжественные мероприятия. Первой была акушерка, принимавшая у нее роды, т. е. она, следуя заведенному порядку, должна была спросить у Агнесс дату рождения. Вторая встреча произошла дюжиной лет позже, когда она ехала на лимузине встречать родителей из нью-йоркского аэропорта. По ходу разговора она сказала водителю, что родители приехали на ее пятидесятилетие. «Если это поспособствует решению, – написала она позже, – они оба были специалистами в тех областях, с которыми я ранее никогда не сталкивалась, и они не обязательно были частью (предположительно большой) группы лиц, которые могли бы быть близки мне по возрасту».

Потому при любых расчетах мы должны согласиться, что две ее встречи были делом поистине удивительным.

Что применимо к дням рождения, применимо и к дням смерти. Реальный случай: три президента – Джон Адамс, Томас Джефферсон и Джеймс Монро – умерли 4 июля. Хм… Джон Адамс и Томас Джефферсон умерли в одном и том же году – в 1826 г. Жутковато. Однако в их времена день 4 июля был особой вехой. Известно, что смерть можно приблизить или отдалить на несколько часов или дней волей человека к жизни или смерти. Так что возможно, что президенты молодой республики просто пытались продержаться до 4 июля, особенно Адамс и Джефферсон, которые дожили до 50-й годовщины подписания Декларации независимости. Потому в этой случайности есть элемент причинности. Никакого совпадения.

Задача об обезьянах возникла, как вопрос статистической механики в теории вероятностей; впервые она была сформулирована в статье Эмиля Бореля «Статистическая механика и необратимость» (Mécanique Statistique et Irréversibilité), опубликованной в 1913 г. Это теорема, которая утверждает, что обезьяна, случайным образом нажимающая на клавиши, напечатает полное собрание сочинений Шекспира, при условии что у нее будет достаточно времени. Конечно, «достаточно времени» может означать бесконечно долгое время. Английский физик сэр Артур Эддингтон был более великодушен в отношении случайности, когда его пригласили дать гиффордовскую лекцию в Эдинбургском университете в 1927 г.: «Если я дам своим пальцам вольно блуждать по клавишам печатной машинки, то «может» случиться так, что из этого моего опуса выйдет вразумительное предложение. Если бы армия обезьян безостановочно стучала по клавишам печатных машинок, то они могли бы написать все книги, хранящиеся в Британском музее» ^{90}.

Давайте пока не будем усложнять задачу. Давайте не будем ожидать библиотеки Британского музея, или полного собрания сочинений, или даже единственного сонета, а только одну строку «shall I compare thee to a summer's day?». Если обезьяна нажмет на клавиши s-h-a-l-l-I-c-o-m-p-a-r-e-t-h-e-e-t-o-a-s-u-m-m-e-r-s-d-a-y именно в таком порядке, мы наверняка сочтем это грандиозным совпадением. Какова вероятность такого события? В самом деле, весьма небольшая! У обезьяны шанс 25 к 1 напечатать первую букву в слове shall, если допустить, что клавиатура ограничена только строчными буквами английского алфавита. А поскольку каждое нажатие на клавишу относительно независимо от других ^{91}, число возможных вариантов того, что обезьяна напечатает первые 5 букв, равняется 26 × 26 × 26 × 26 × 26 = 11 881 376, или шанс 11 881 375 к 1. Но это шанс выполнить задачу с первой попытки. Бедному животному надо дать больше, чем только один шанс. Много больше. Рассмотрим вероятность невыполнения задачи с первой попытки. Она составит 1 – (1/26)⁵ ≈ 0,99999991583, т. е. близка к достоверности. После N попыток вероятность того, что она не нажмет клавиши в нужном порядке, составит (1 – (1/26)⁵)^N.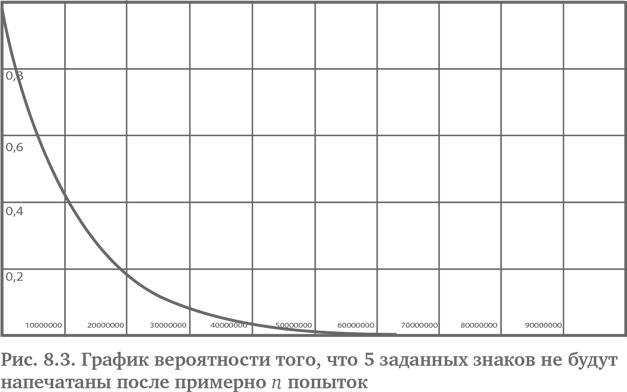

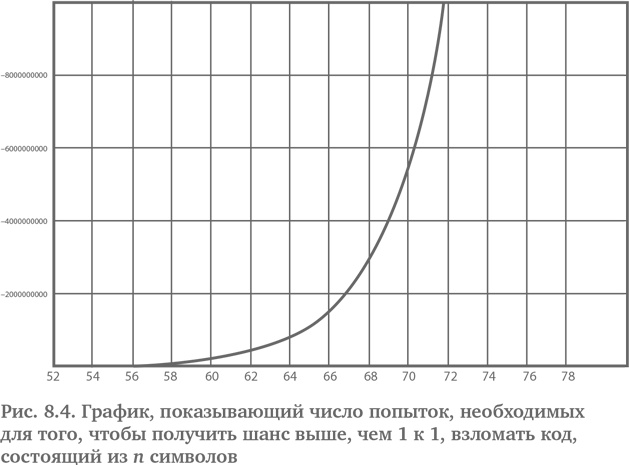
При N = 8 235 542 у нее будет шанс выше, чем 1 к 1, напечатать первое слово из шекспировского сонета. Рис. 8.3 ^{92} показывает, как вероятность не напечатать слово shall приближается к нулю после примерно 50 млн попыток.

Попробуйте приложить это к парольной защите. Значит, компьютерная программа, которая подбирает буквы случайным образом, может легко взломать пароль, состоящий из 5 символов. В наши дни даже относительно слабый центральный процессор может перебрать 50 млн попыток меньше чем за 10 сек. Но если вы добавите всего один символ, то для того, чтобы иметь шанс подбора выше, чем 1 к 1, потребуется уже не менее 214 124 096 попыток. С каждым дополнительным символом (включая комбинации букв, чисел и символов или изменение регистра) сложность растет экспоненциально (см. рис. 8.4).

Вероятность случайного подбора первых 6 цифр π с числовой клавиатуры – 0,000001, или шанс один на миллион. Существует шанс выше, чем 1 к 1, что одна из тысячи обезьян нажмет первые 6 цифр π, если каждой из обезьян дать 1000 попыток. Возможно, π – не такое уж особенное число. Конечно, мы берем только первые 6 цифр π. Возьмем первые 100 цифр π. Даже если каждая песчинка на Земле и каждая звезда во Вселенной станут случайным образом подбирать цифры до конца времен, вероятность написания π до сотого знака практически не сдвинется с нуля. В 1913 г. Эмиль Борель предложил нам представить миллион обезьян, случайным образом стучащих по клавишам печатной машинки по 10 часов в день ^{93}.