Вселенная. Курс выживания среди черных дыр, временных парадоксов, квантовой неопределенности - читать онлайн книгу. Автор: Дэйв Голдберг, Джефф Бломквист cтр.№ 55

На рис. 11.4 показан один из вариантов, как мы можем представить распространение частицы, обладающей массой. Частица на рисунке перескакивает из точки А в точку В за несколько стадий. Она переходит из точки А в точку 1, из точки 1 в точку 2 и так далее, пока, наконец, не попадает из точки 6 в точку В. Интересно, однако, что в таком виде правило для каждого скачка – это правило для частицы с нулевой массой, но с одной важной оговоркой: каждый раз, когда частица меняет направление, мы должны применить новое правило уменьшения циферблата, причем величина уменьшения обратно пропорциональна массе описываемой частицы. Это значит, что при каждом переводе часов циферблаты, связанные с тяжелыми частицами, уменьшаются менее резко, чем циферблаты, связанные с более легкими частицами. Важно подчеркнуть, что это правило системное.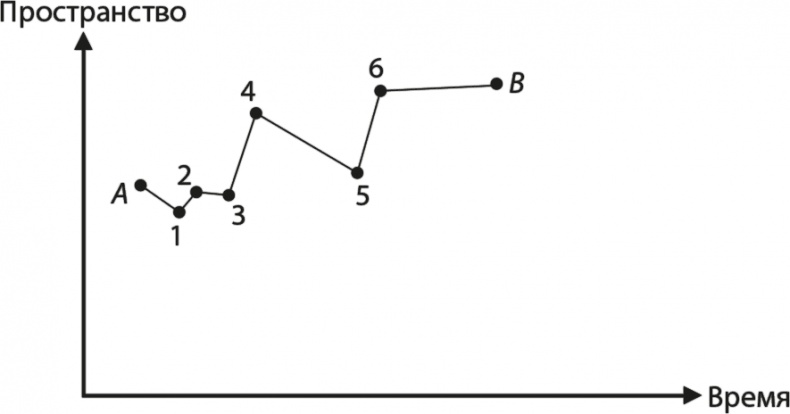

Рис. 11.4. Массивная частица, движущаяся из точки А в точку В

И зигзагообразное движение, и уменьшение циферблата непосредственно вытекают из правил Фейнмана для распространения массивной частицы без каких-то других предположений ^[52]. На рис. 11.4 показан лишь один способ попадания частицы из точки А в точку В – после шести поворотов и шести уменьшений. Чтобы получить итоговый циферблат, связанный с массивной частицей, переходящей из точки А в точку В, мы, как всегда, должны сложить бесконечное количество циферблатов, связанных со всеми возможными способами, которыми частица может проделать свой зигзагообразный путь из точки А в точку В. Самый простой способ – прямой путь без всяких поворотов, но придется принять во внимание и маршруты с огромным количеством поворотов.

Для частиц с нулевой массой уменьшающий коэффициент, связанный с каждым поворотом, просто убийственен, потому что бесконечен. Иными словами, после первого же поворота мы уменьшаем циферблат до нуля. Таким образом, для частиц без массы имеет значение только прямой маршрут – другим траекториям просто не соответствует никакой циферблат. Именно этого мы и ожидали: для частиц без массы мы можем использовать правило скачка. Однако для частиц с ненулевой массой повороты разрешены, хотя если частица очень легкая, то коэффициент уменьшения налагает суровое вето на траектории со многими поворотами.

Таким образом, наиболее вероятные маршруты содержат мало поворотов. И наоборот, тяжелым частицам не грозит слишком большой уменьшающий коэффициент при повороте, так что они чаще описываются маршрутами с зигзагообразным движением. Поэтому можно считать, что тяжелые частицы можно считать частицами без массы, которые двигаются из точки А в точку В зигзагообразно. Количество зигзагов – это и есть то, что мы называем «массой».

Все это замечательно, потому что теперь у нас появился новый способ представления массивных частиц. На рис. 11.5 показано распространение трех разных частиц с возрастающей массой из точки А в точку В. Во всех случаях правило, связанное с каждым «зигзагом» их пути, совпадает с правилом для частицы без массы, и за каждый поворот приходится расплачиваться уменьшением циферблата. Но не следует слишком радоваться: пока мы еще не объяснили ничего фундаментального. Все, что пока удалось сделать, – это заменить слово «масса» словами «стремление к зигзагам». Это можно было сделать, потому что оба варианта – математически эквивалентные описания распространения массивной частицы. Но даже при таких ограничениях наши выводы кажутся интересными, а сейчас мы узнаём, что это, оказывается, не просто математический курьез.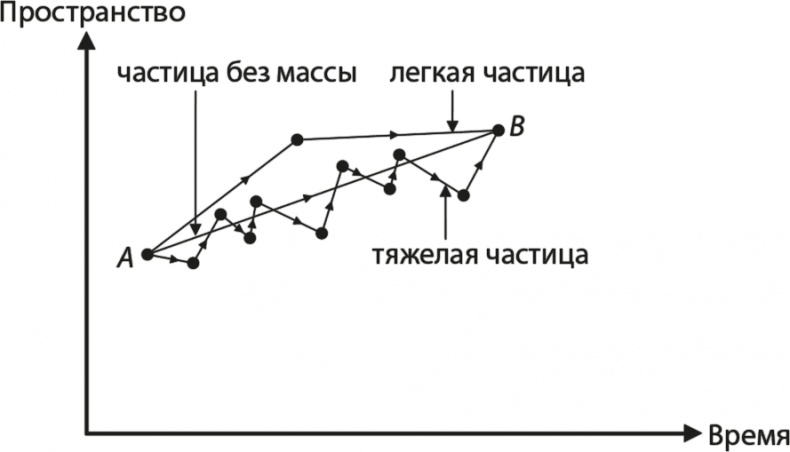

Рис. 11.5. Частицы с возрастающей массой движутся из точки А в точку В. Чем более массивна частица, тем больше зигзагов в ее движении

Перенесемся в царство умозрительного – хотя к тому моменту, когда вы будете читать эту книгу, теория может уже и получить свое подтверждение.

В настоящий момент на БАК совершаются столкновения протонов общей энергией в 7 ТэВ. ТэВ – это тераэлектронвольты, что соответствует энергии, которую имел бы электрон, пропущенный через разность потенциалов в 7 000 000 миллионов вольт. Для сравнения отметим, что примерно такова энергия, которую субатомные частицы имели через триллионную долю секунды после Большого взрыва, и этой энергии достаточно, чтобы создать прямо из воздуха массу, эквивалентную массе 7000 протонов (в соответствии с формулой Эйнштейна E = mc²). И это лишь половина расчетной энергии: при необходимости БАК может включить и более высокие обороты.

Одна из основных причин, по которым 85 стран всего мира соединили силы, создали этот гигантский дерзкий эксперимент и управляют им, – стремление найти механизм, отвечающий за создание массы фундаментальных частиц. Наиболее распространенная идея происхождения массы состоит в ее связи с зигзагами и устанавливает новую фундаментальную частицу, на которую «наталкиваются» другие частицы в своем движении по Вселенной. Эта частица – бозон Хиггса. В соответствии со Стандартной моделью, без бозона Хиггса фундаментальные частицы перескакивали бы с места на место без всяких зигзагов, и Вселенная была бы совсем иной. Но если мы заполним пустое место частицами Хиггса, они смогут отклонять частицы, заставляя их совершать зигзаги, что, как мы уже установили, ведет к появлению «массы». Примерно так, как вы идете через переполненный бар: вас толкают то слева, то справа, и вы практически зигзагами пробираетесь к стойке.

Механизм Хиггса получил свое имя в честь эдинбургского теоретика Питера Хиггса; это понятие было введено в физику частиц в 1964 году. Идея, очевидно, носилась в воздухе, потому что ее высказали в одно и то же время сразу несколько человек: во-первых, конечно, сам Хиггс, а также Роберт Браут и Франсуа Энглер, работавшие в Брюсселе, и лондонцы Джеральд Гуральник, Карл Хейган и Том Киббл. Их работы, в свою очередь, основывались на более ранних трудах многих предшественников, в том числе Вернера Гейзенберга, Ёитиро Намбу, Джеффри Голдстоуна, Филипа Андерсона и Стивена Вайнберга. Полное осмысление этой идеи, за которое в 1979 году Шелдон Глэшоу, Абдус Салам и Вайнберг получили Нобелевскую премию, – это и есть не что иное, как Стандартная модель физики частиц. Сама идея довольно проста: пустое место на самом деле не пусто, что и приводит к зигзагообразному движению и появлению массы. Но нам, очевидно, нужно еще многое объяснить. Как же оказалось, что пустое место вдруг стало набито частицами Хиггса, – разве мы не заметили бы этого раньше? И как это странное состояние вещей вообще возникло? Предложение действительно кажется довольно экстравагантным. Кроме того, мы не объяснили, почему у некоторых частиц (например, у фотонов) нет массы, а другие (W-бозоны и топ-кварки) обладают массой, сопоставимой с массой атома серебра или золота.