Вселенная. Курс выживания среди черных дыр, временных парадоксов, квантовой неопределенности - читать онлайн книгу. Автор: Дэйв Голдберг, Джефф Бломквист cтр.№ 27

Возможно, вас интересует, почему эти конкретные волны называются стоячими. Дело в том, что они не меняют своей формы. Если мы сделаем два снимка гитарной струны, колеблющейся в форме стоячей волны, то эти две фотографии будут отличаться только общим размером волны. Пики будут всегда находиться в одних и тех же местах, как и узлы, которые фиксируются концами струны или, в случае с бассейном, его бортиками.

С математической точки зрения можно сказать, что волны на двух фотографиях отличаются только общим множителем. Этот множитель периодически колеблется со временем и отражает ритмические колебания струны. То же самое верно и для бассейна на рис. 6.1, где каждая фотография отличается от остальных общим множителем. Например, последняя фотография может быть получена из первой посредством умножения высоты волны в каждой точке на −1.

Иными словами, волны, каким-то образом ограниченные, всегда можно выразить в виде суммы стоячих волн (то есть тех, которые не меняют своей формы), и, как мы уже сказали, есть довольно серьезные причины посвятить им столько времени. Главная из них – стоячие волны квантованы. Это совершенно очевидно для стоячих волн на гитарной струне: длина основного тона в два раза превышает длину струны, а следующая по длине возможная волна равняется длине струны. Между этими двумя волнами стоячей волны с какой-либо промежуточной длиной быть не может, так что можно сказать, что разрешенные длины волн на гитарной струне квантованы.

Таким образом, с помощью стоячих волн проявляется следующее: «запирая» волны, мы что-то квантуем. В случае с гитарной струной это, очевидно, длина волны. В случае с электроном внутри ящика квантовые волны, соответствующие электрону, тоже будут заперты, и по аналогии можно ожидать, что в ящике будут присутствовать лишь волны с определенным, конкретным набором длин волн, а, следовательно, нечто вновь будет квантовано. Другие волны просто не могут существовать, как гитарная струна не может одновременно звучать всеми нотами в октаве. И общее состояние электрона, как и звук гитары, описывается смешением стоячих волн. Эти квантовые стоячие волны начинают выглядеть очень интересно. Заинтригованы? Приступаем к анализу.

Чтобы продвинуться в своих исследованиях, мы должны уточнить форму ящика, в который помещаем наш электрон. Для простоты предположим, что электрон может свободно двигаться в области размером L, но ему полностью запрещено выходить за пределы этой области. Необязательно уточнять, каким образом мы собираемся запретить электрону это делать, но, если наша модель претендует на то, чтобы быть упрощенной моделью атома, нужно представить, что за это отвечает притяжение положительно заряженного ядра. На научном жаргоне это имеет название «прямоугольная потенциальная яма». Мы зарисовали эту ситуацию на рис. 6.3, и причины для такого названия представляются очевидными. Идея заключения частицы в потенциальной яме очень важна, мы обратимся к ней еще не раз, поэтому полезно убедиться, что мы точно понимаем, о чем идет речь. Как на самом деле можно улавливать частицы?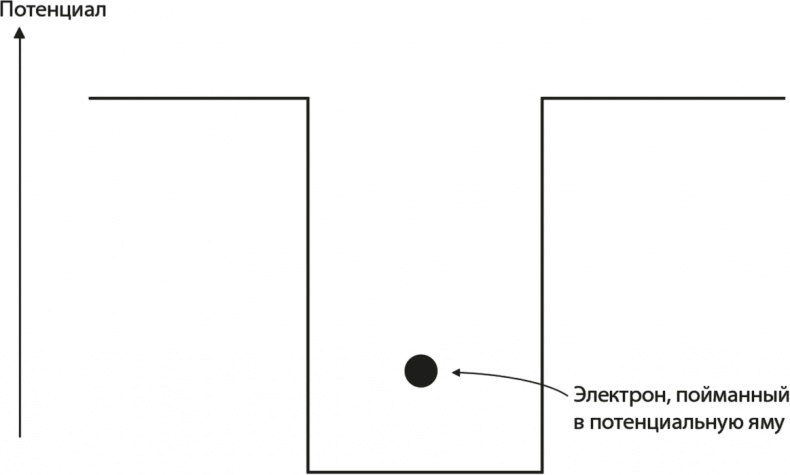

Рис. 6.3. Электрон, пойманный в прямоугольную потенциальную яму

Вопрос довольно сложный: чтобы добраться до его сути, нужно выяснить, как частицы взаимодействуют друг с другом, о чем пойдет речь в главе 10. Тем не менее мы можем добиться прогресса в рассуждениях, если не будем задавать слишком много вопросов.

Способность «не задавать слишком много вопросов» – необходимый для физика навык, потому что для получения хоть каких-то ответов где-то надо провести черту, так как ни одна система объектов не может быть полностью изолированной. Кажется разумным, что при желании понять, как работает микроволновая печь, не стоит интересоваться движением вокруг нее.

Все это движение окажет незначительное влияние на работу микроволновки. Оно вызовет колебания воздуха и земли, которые повлекут за собой небольшие сотрясения и самой печи. Могут появиться какие-то бродячие магнитные поля, которые повлияют на работу электроники, как бы хорошо она ни была защищена от подобных воздействий. Игнорируя такие вещи, легко допустить ошибку, так как можно упустить из виду действительно важные детали. Если так и произойдет, мы получим неверный ответ и будем вынуждены пересмотреть предположения. Это очень важный момент, напрямую связанный с научным успехом: все предположения в конце концов подтверждаются или опровергаются экспериментально. Арбитром является природа, а не человеческая интуиция. Поэтому наша стратегия – игнорировать подробности функционирования механизма удержания электрона и моделировать нечто под названием «потенциал». Слово «потенциал» на самом деле обозначает «воздействие на частицу какой-то физической или иной силы, которую я не очень хочу подробно объяснять». Мы, впрочем, позже подробно опишем методы взаимодействия частиц, а пока будем употреблять термин «потенциал». Если это звучит несколько бесцеремонно, рассмотрите пример, иллюстрирующий использование потенциалов в физике.

На рис. 6.4 изображен мяч, лежащий в долине. Если ударить по мячу, он может подняться, но лишь до определенного предела, после чего снова упадет. Это отличный пример частицы, пойманной потенциалом. В этом случае гравитационное поле Земли создает потенциал, а крутой холм порождает крутой потенциал. Нужно понимать, что мы можем вычислить подробности передвижения мяча по долине, не зная деталей того, как долина взаимодействует с мячом, потому что для этого пришлось бы знать еще и теорию квантовой электродинамики. Если окажется, что детали внутриатомного взаимодействия между атомами в долине и атомами в мяче слишком сильно воздействуют на движение мяча, наши предсказания окажутся неверными. На самом деле внутриатомные взаимодействия важны, потому что из них возникает трение, но моделировать ситуацию можно и без обращения к диаграммам Фейнмана. Однако мы уклонились от темы.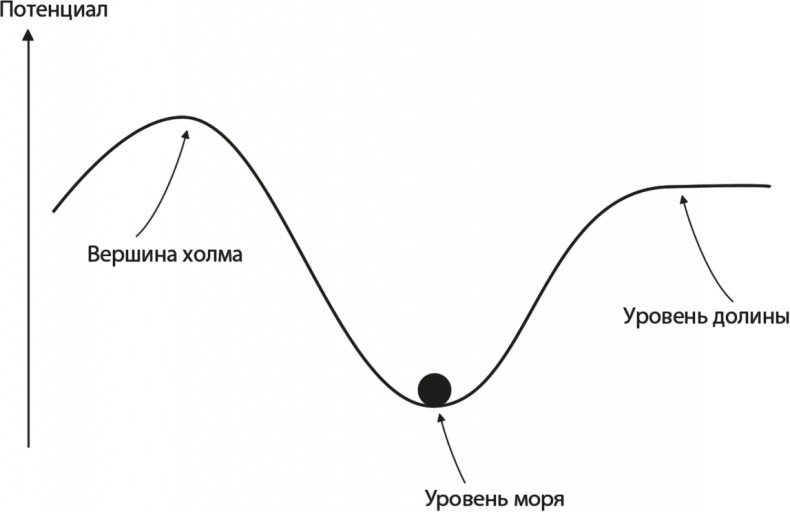

Рис. 6.4. Мяч лежит в долине. Высота над уровнем моря прямо пропорциональна потенциалу, воздействию которого подвергается движущаяся частица

Этот пример очень важен, потому что в прямом смысле демонстрирует форму потенциала ^[23].

Однако идея имеет более общее содержание и работает в том числе и для потенциалов, созданных не гравитацией и не впадинами на земной поверхности. Примером служит электрон, оказавшийся в прямоугольной яме. В отличие от случая с мячом в долине, высота стенок ящика не может быть точной высотой чего бы то ни было; скорее, можно говорить, что она соответствует скорости, с которой должен двигаться электрон, чтобы выбраться из ямы. В случае с долиной аналогом этого будет быстрое движение мяча, при котором он взлетит выше стен и выскочит из ямы. Если электрон движется достаточно медленно, точная высота потенциала не имеет особого значения, и можно уверенно предположить, что движение электрона ограничено внутренней частью ямы.