На плечах гигантов - читать онлайн книгу. Автор: Стивен Хокинг cтр.№ 39

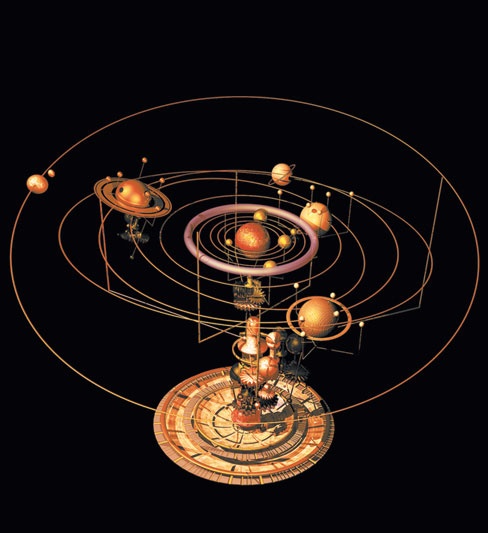
Модель Солнечной системы в стиле ньютоновских времен, однако с добавлением пояса астероидов, который был открыт позднее.

Я производил подобный опыт с магнитом и железом: если их поместить каждый в отдельный сосуд и пустить плавать на спокойной воде так, чтобы сосуды взаимно касались, то ни тот, ни другой не приходят в движение, но вследствие равенства взаимного притяжения сосуды испытывают равные давления и остаются в равновесии.

Подобным образом и притяжение между Землею и отдельными ее частями взаимно. Вообразим, что Земля рассечена какою-либо плоскостью EG на две части EGF и EGJ – притяжения их друг другом будут равны. В самом деле, если отсечь другою плоскостью НК, параллельной EG, от части EGJ часть HKJ, равную EFG, то ясно, что средняя часть EGKH не будет испытывать ни от одной из крайних большего притяжения, нежели от другой, и будет находиться между ними как бы подвешенной, оставаясь в равновесии и покое. Но вся крайняя часть HKJ всем своим весом давит на среднюю EGHK и побуждает ее двигаться в сторону другой крайней EFG, следовательно, сила, с которою сумма частей EGHK и HKJ, т. е. EGJ, стремится к EFG, равна весу (притяжению) части HKJ, т. е. весу части EFG, следовательно, притяжения друг к другу, т. е. веса частей GEF и GEJ друг на друге, между собою равны, что я и имел в виду показать. Если бы эти веса не были между собою равны, то вся Земля, плавающая в свободном эфире, уступила бы большему весу и под его действием ушла бы в бесконечность.

Подобно тому как при ударе и отражении тела, коих скорости обратно пропорциональны массам, равнозначащи, так и при движении механических приборов действующие силы, коих скорости, взятые по направлению самих сил (проекции скорости точки приложения каждой силы на направление этой силы), обратно пропорциональны этим силам, равнозначащи между собою и при стремлении в противоположные стороны взаимно уравновешиваются. Таким образом в стремлении привести в движение коромысло весов равнозначащи грузы, обратно пропорциональные тем направленным прямо вверх или вниз скоростям, кои они получают при качаниях коромысла, т. е. грузы, поднимающиеся или опускающиеся вертикально, равнозначащи, если они обратно пропорциональны расстояниям их точек подвеса от ребра опоры коромысла. Если же эти грузы поднимаются или опускаются по наклонным плоскостям или по иным препятствиям, то они равнозначащи, когда они обратно пропорциональны проекциям подъема или опускания на отвесное направление, т. е. на направление силы тяжести.

Подобно этому в блоке или полиспасте усилие руки, тянущей снасть прямо, удержит прямо или наклонно поднимаемый груз в равновесии, если это усилие будет так относиться к весу груза, как скорость отвесного подъема груза относится к скорости руки, тянущей снасть. В часах и подобных им механизмах, состоящих из сцепленных между собою колес, две силы, взаимно противящиеся, т. е. такие, из коих одна способствует, другая же сопротивляется движению, находятся в равновесии, если эти силы обратно пропорциональны скоростям тех частей колес, к коим они приложены. Сила винта, сжимающего тело, так относится к усилию руки, вращающей рукоятку, как окружная скорость той точки рукоятки, где усилие руки приложено, относится к скорости поступания винта против сжимаемого тела. Силы, с коими клин раздвигает две части раскалываемого дерева, так относятся к силе молота, бьющего по клину, как скорость перемещения клина в направлении действующей от бьющего его молота силы относится к скоростям, с которыми части дерева уступают клину, причем эти скорости надо брать по направлениям, перпендикулярным к щекам клина. Совершенно подобно соотношение между силами и во всякого рода машинах. Действительность и назначение машин в том только и состоит, чтобы, уменьшая скорость, увеличивать силу, и наоборот, ибо во всех подобного рода приборах, в сущности, решается такая задача: заданный груз двигать заданною силою или же заданное сопротивление преодолеть заданным усилием.

В самом деле, если машина будет устроена таким образом, чтобы скорости точек приложения движущей силы и сопротивления были обратно пропорциональны этим силам, то движущая сила уравновесит сопротивление, при бóльшем же отношении скоростей преодолеет его. Если отступление от пропорциональности скоростям будет таково, что будут преодолеваться сопротивления, происходящие от трения соприкасающихся и скользящих друг по другу тел, от сцепления тел непрерывных и разъединяемых и от подъема грузов, то, за выключением всех этих сопротивлений, избыточная сила произведет ускорение, пропорциональное ее величине как в частях машины, так и в сопротивляющемся теле.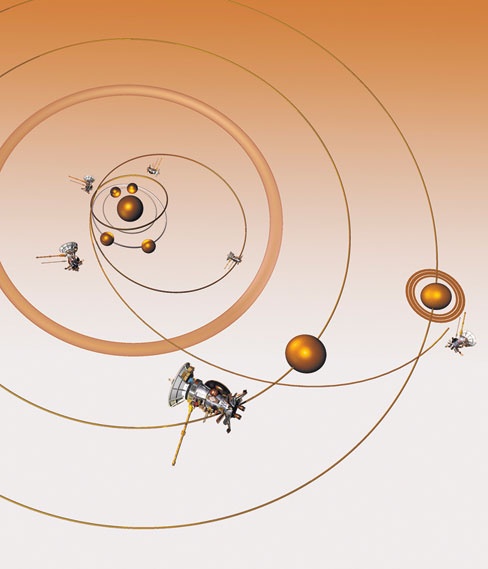

Межпланетная траектория космического аппарата «Кассини». Чтобы при запуске космических аппаратов рассчитать их траектории, орбиты и гравитационные маневры, иначе называемые «эффектом рогатки», нужна очень сложная математика. Однако эти расчеты целиком и полностью опираются на теоретические модели Нью-тона, которым уже больше трехсот лет. Сложные расчеты орбит и успешный спуск космического зонда на Титан – яркое свидетельство масштабности научных достижений Ньютона.

Дальнейшее изложение учения о машинах сюда не относится, я хотел лишь показать, сколь далеко простирается и сколь благонадежен третий закон движения. Если действие движущей силы оценивать пропорционально произведению этой силы и скорости и, подобно этому, противодействие сопротивлений оценивать для каждой части в отдельности пропорционально произведению ее скорости и встречаемого ею сопротивления, происходящего от трения, сцепления, веса и ускорения, то во всякой машине действие и противодействие будут постоянно равны, и поскольку действие передается машиною и в конце концов прилагается к сопротивляющемуся телу, то это последнее его значение будет обратно значению противодействия.

Правила умозаключений в физике Правило I

Не должно принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений.

По этому поводу философы утверждают, что природа ничего не делает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим. Природа проста и не роскошествует излишними причинами вещей.

Правило II

Поэтому, поскольку возможно, должно приписывать те же причины того же рода проявлениям природы.

Так, например, дыханию людей и животных, падению камней в Европе и в Африке, свету кухонного очага и Солнца, отражению света на Земле и на планетах.

Правило III

Такие свойства тел, которые не могут быть ни усиляемы, ни ослабляемы и которые оказываются присущими всем телам, над которыми возможно производить испытания, должны быть почитаемы за свойства всех тел вообще.

Свойства тел постигаются не иначе, как испытаниями; следовательно, за общие свойства надо принимать те, которые постоянно при опытах обнаруживаются и которые, как не подлежащие уменьшению, устранены быть не могут. Понятно, что в противность ряду опытов не следует измышлять на авось каких-либо бредней, не следует также уклоняться от сходственности в природе, ибо природа всегда и проста и всегда сама с собой согласна.