О том, чего мы не можем знать. Путешествие к рубежам знаний - читать онлайн книгу. Автор: Маркус Дю Сотой cтр.№ 14

Cтраница 14

Удивительное положение. Уравнения, открытые наукой, дают совершенно детерминистическое описание эволюции многих динамических систем, подобных погоде. И тем не менее во многих случаях предсказания, которые можно из них получить, нам недоступны, так как любые измерения положения или скорости полета частицы могут быть лишь приближениями к истинным условиям.

Именно поэтому, когда британская метеорологическая служба составляет прогноз погоды, она берет данные, зарегистрированные метеостанциями, разбросанными по всей стране, и, вместо того чтобы использовать их в уравнениях, метеорологи производят несколько тысяч модельных расчетов, варьируя данные в некотором диапазоне значений. В течение некоторого времени прогнозы остаются достаточно близкими, но начиная приблизительно с пятого дня от текущей даты результаты зачастую расходятся так далеко друг от друга, что один набор данных может предсказывать приход в Великобританию аномально жаркой погоды, в то время как изменение нескольких знаков после запятой дает предсказание ливней, которые затопят всю страну.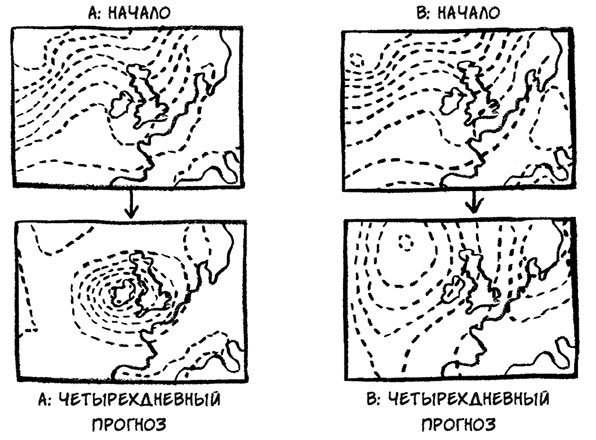

Исходя из почти одинаковых начальных условий, прогноз А предсказывает, что через четыре дня на всех Британских островах будут сильные ветры и дожди, а прогноз В – приход с Атлантики зоны высокого давления

Великий шотландский физик Джеймс Клерк Максвелл сформулировал в своей книге «Материя и движение», опубликованной в 1873 г., важное отличие системы детерминистической, но непознаваемой: «Существует принцип, на который часто ссылаются: “Одинаковые причины всегда производят одинаковые следствия”» ^[27]. Это безусловно справедливо в отношении математического уравнения, описывающего динамическую систему. Но Максвелл продолжает: «Существует другой принцип, который не следует смешивать с приведенным [выше]: “Подобные причины производят подобные следствия”. Это справедливо лишь в том случае, если небольшие изменения начальных условий производят лишь небольшие изменения в конечном состоянии системы». Ложность именно этого принципа выявило в XX в. открытие теории хаоса.

Такая чувствительность к малым изменениям начальных условий может сорвать мои попытки использовать выписанные мной уравнения для предсказания будущего игральной кости. Уравнения у меня есть, но могу ли я быть уверен в точности определения угла, под которым кубик вылетает из моей руки, скорости его вращения, расстояния до стола?

Конечно, не все так уж безнадежно. Бывают случаи, в которых малые изменения не приводят к разительным отклонениям результатов уравнений, как в примере траекторий на классическом бильярдном столе. Важно осознавать, когда познание невозможно. Прекрасный пример осознания момента, начиная с которого невозможно узнать, что произойдет дальше, был открыт математиком Робертом Мэем, когда он анализировал уравнения роста популяций.

Мэй, родившийся в 1938 г. в Австралии, сначала учился физике и работал в области сверхпроводимости. Но в конце 1960-х гг. в его научной работе произошел резкий поворот, когда он познакомился с вновь образованным движением социальной ответственности в науке. Его интересы переместились с поведения групп электронов на более актуальные вопросы закономерностей динамики популяций животных. В то время биология еще не была естественной средой для человека с математическим складом ума, но работы Мэя впоследствии изменили это положение. Его великое открытие стало возможным благодаря сочетанию строгого математического образования, которое он получил как физик, и нового интереса к проблемам биологии.

В опубликованной в 1976 г. в журнале Nature статье под названием «Простые математические модели с чрезвычайно сложной динамикой» ^[28] Мэй рассмотрел динамику математического уравнения, описывающего циклический рост популяции. Он показал, что даже вполне невинно выглядящее уравнение может давать численные результаты с необычайно сложным поведением. Его формула популяционной динамики была не каким-нибудь сложным дифференциальным уравнением, а простым дискретным уравнением с обратной связью, которое мог обсчитать кто угодно при помощи карманного калькулятора.

Уравнение динамики популяции с обратной связью

Рассмотрим популяцию животных, численность которой может варьироваться от нуля до некоторого гипотетического максимального значения, обозначенного N. Существует некоторая доля Y этого максимума (лежащая между 0 и 1), определяющая в уравнении, какая часть популяции выживет к следующему циклу с учетом воспроизводства и борьбы за пищевые ресурсы. Предположим, что коэффициент воспроизводства в каждом цикле равен r. Тогда, если доля максимальной численности популяции, выжившая к концу цикла, была равна Y, то численность следующего поколения составит r · Y · N.

Но выживут не все вновь появившиеся животные. Согласно этому уравнению, доля не выживших животных также будет равна Y. То есть из r · Y · N животных, существовавших в начале цикла, умрет Y(r · Y · N). Значит, всего к концу цикла останется в живых (r · Y · N) – (r · Y ² · N) = [r · Y(1 – Y)] · N животных, а доля максимальной численности популяции, существующая в текущем цикле, равна r · Y(1 – Y).

По сути дела, эта модель предполагает, что произведение численности выжившей к концу каждого цикла части популяции на постоянный коэффициент r, называемый коэффициентом воспроизводства, дает число животных, существующих в начале следующего цикла. Но необходимых для выживания ресурсов на всех не хватает. Поэтому уравнение вычисляет, какая часть этих животных доживет до конца цикла. Полученное число выживших животных снова умножают на коэффициент r, что дает численность следующего поколения. Интересная особенность этого уравнения состоит в том, что его поведение сильно зависит от выбора значения r, коэффициента воспроизводства. Некоторые значения r дают в высшей степени непредсказуемое поведение. Мы можем точно знать, как будут изменяться значения. Но существует некий предел, за которым они полностью выходят из-под контроля. Знание внезапно оказывается недостижимым, так как добавление всего одного лишнего животного может привести к резкому изменению динамики численности популяции.

Например, Мэй выяснил, что при значениях r от 1 до 3 численность популяции в конце концов стабилизируется. В этом случае, каковы бы ни были начальные условия, численность будет постепенно стремиться к некоторому постоянному значению, зависящему от величины r. Это похоже на игру на бильярде, в центре которого устроена воронка. Куда бы я ни запустил шар, рано или поздно он окажется на дне воронки.