Магия математики. Как найти x и зачем это нужно | Артур Бенджамин | страница 9 | LoveRead.ec

a(b + c) = ab + ac.

Это правило следует использовать при умножении однозначного числа на двузначное, например,

7 × 28 = 7 × (20 + 8) = (7 × 20) + (7 × 8) = 140 + 56 = 196.

Очень полезная штука, когда дело доходит до счета. Допустим, у нас есть 7 кошельков с монетами: по 20 золотых и 8 серебряных монет в каждом. Сколько у нас всего монет? С одной стороны, можно подойти к проблеме так: в каждом кошельке по 28 монет, значит, всего их 7 × 28. С другой стороны, можно посчитать отдельно монеты разного достоинства: 7 × 20 золотых и 7 × 8 серебряных, значит, всего: (7 × 20) + (7 × 8). Следовательно, 7 × 28 = (7 × 20) + (7 × 8).

Закон дистрибутивности можно выразить и геометрически, начертив прямоугольник и разбив его на два части, как на рисунке.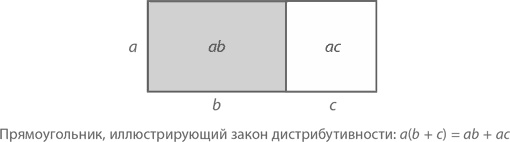

Магия математики. Как найти x и зачем это нужно

Как видим, площадь прямоугольника равна a(b + c). Однако левая часть выглядит как ab, правая – как ac, поэтому в итоге у нас получается ab + ac. Отличная иллюстрация к закону дистрибутивности при условии, что a, b и c – положительные величины.

Иногда, кстати, его можно применить одновременно и к числам, и переменным, например,

3(2x + 7) = 6x + 21

«Читать» это уравнение можно двумя способами: слева направо и справа налево. В первом случае мы видим 3, умноженное на 2x + 7. Во втором мы разлагаем 6x + 21 на сомножители, «вытягивая» тройку из 6x и 21.

Отступление

Почему «минус» на «минус» при умножении дают «плюс»? Иными словами, с чего бы вдруг (–5) × (–7) = 35? У учителей всегда наготове с десяток самых разных объяснений, начиная с аннулирования долгов и заканчивая железобетонным «ну, потому что вот так». Но настоящая причина – в том, что закон дистрибутивности работает по отношению ко всем числам, не только положительным. А раз уж мы применяем его и к отрицательным числам (и к нолю, кстати), будьте готовы столкнуться с последствиями. Давайте посмотрим, почему.

Допустим, мы примем тот факт, что –5 × 0 = 0, а –5 × 7 = –35. (Для этих примеров тоже имеются свои доказательства, очень близкие к тому, что мы выстраиваем сейчас, но большинство с радостью просто принимают эти утверждения на веру.) Взгляните-ка вот на что:

– 5 × (–7 + 7)

Чему это равно? С одной стороны, это все то же –5 × 0, равное, как нам хорошо известно, нолю. С другой стороны, использовав закон дистрибутивности, мы получим ((–5) × (–7)) + (–5 × 7). Следовательно,

((–5)) × ((–7)) + (–5 × 7) = ((–5) × (–7)) – 35 = 0

А если ((–5) × (–7)) – 35 = 0, мы вынуждены признать, что (–5) × (–7) = 35. Обобщая, можно сказать, что закон дистрибутивности утверждает, что для всех значений a и b будет верно следующее: (–a) × (–b) = ab.

Магия метода FOIL

Одним из самых важных и полезных следствий из закона дистрибутивности является алгебраическое правило FOIL^[3], согласно которому для любых переменных a, b, c, d верно следующее:

(a + b)(c + d) = ac + ad + bc + bd

Смотрите, как правило FOIL работает на практике: cначала мы перемножаем первые числа в (a + b)(c + d), то есть ac. Потом – внешние, то есть ad. Затем – внутренние: bc. И наконец – последние: bd.

Давайте проиллюстрируем все это примером с конкретными числами:

23 × 45 = (20 + 3)(40 + 5) = (20 × 40) + (20 × 5) + (3 × 40) + (3 × 5) = 800 + 100 + 120 + 15 = 1035

Отступление

Почему работает правило FOIL? Согласно закону дистрибутивности (по отношению к части со сложением, идущей на первом месте),

(a + b)e = ae + be

А теперь вместо e подставим c + d, что даст нам

(a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd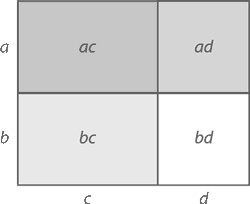

Последняя часть становится возможной благодаря повторному применению закона дистрибутивности. Если вы предпочитаете геометрически визуализированное доказательство (при условии, что a, b, c, d – положительные величины), то вот вам прямоугольник, площадь которого можно найти двумя различными способами.

С одной стороны, площадь можно высчитать с помощью (a + b)(c + d). С другой – мы можем разбить большой прямоугольник на четыре с площадями ac, ad, bc и bd. Значит, общая площадь будет равна ac + ad + bc + bd. Знак равенства между двумя этими подходами обеспечивает правило FOIL.

А теперь давайте посмотрим, как работает магия правила FOIL. Бросьте две игральные кости и посмотрите таблицу, которая приведена чуть ниже. Допустим, вы выкинули 6 и 3. На обратных сторонах костей будет, соответственно, 1 и 4.

В нашем примере результат будет равен 49. И сколько бы вы ни бросали обычные шестигранные кости, результат будет тот же. Дело в том, что сумма чисел на противоположных сторонах стандартной игральной кости всегда равна 7. То есть если обозначить выпавшие числа буквами x и y, их парами будут 7 – x и 7 – y. Алгебра переделывает нашу таблицу таким вот образом:

Магия математики. Как найти x и зачем это нужно - читать онлайн книгу. Автор: Артур Бенджамин cтр.№ 9

Онлайн книга - Магия математики. Как найти x и зачем это нужно | Автор книги - Артур Бенджамин