
|
||
|
|
||
|
|
Онлайн книга - Магия математики. Как найти x и зачем это нужно | Автор книги - Артур Бенджамин
Cтраница 65

cos (90° – B) = cos 90° cos B + sin 90° sin B = sin B Происходит это на том основании, что cos 90° = 0, а sin 90° = 1. Если в этом уравнении заменить B на 90° – B, получим cos B = cos 90° cos (90° – B) + sin 90° sin (90° – B) = sin (90° – B) Мы уже доказали правдивость этих утверждений на примере B как острого угла. Однако алгебра позволяет нам пойти дальше и подтвердить их для любого значения B. Так, если заменить B на – B, мы придем к cos (A + B) = cos A cos (–B) + sin A sin (–B) = cos A cos B – sin A sin B так как cos (–B) = cos B, а sin (–B) = –sin B. Если предположить, что B = A, у нас получится формула функций двойного угла: cos (2A) = cos² A – sin² A А так как cos² A = 1 – sin² A и sin² A = 1 – cos² A, мы также можем утверждать, что cos (2A) = 1 – 2 sin² A и cos (2A) = 2 cos² A – 1 Из этого тождества косинусов проистекает аналогичное тождество синусов, например, sin (A + B) = cos (90 – (A + B) = cos ((90 – A) – B) = cos (90 – A) cos B + sin (90 – A) sin B = sin A cos B + cos A sin B B = A приводит нас к формуле функций двойного угла для синусов – sin (2A) = 2 sin A cos A а замена B на – B – к sin (A – B) = sin A cos B – cos A sin B Давайте соберем в одну таблицу все тождества, которые мы успели вывести в этой главе: 
Повторюсь: использовать буквы A и B вы не обязаны, сгодятся и любые другие (скажем, cos (2u) = cos²u – sin²u или sin (2θ) = 2 sin θ cos θ). Радианы и графики в тригонометрии
До сих пор нам встречались углы, значения которых находились исключительно в диапазоне от 0 до 360 градусов. Но пристальный взгляд на единичную окружность невольно заставляет усомниться в обоснованности выбора числа 360. Сделан он был давным-давно, еще в древнем Вавилоне, где в обиходе была шестидесятеричная система счисления, использовавшаяся в том числе и в календаре (да-да, число 360 подозрительно напоминает количество дней в году). Альтернатива была предложена много позже, в XIX веке, когда в математике – а затем и в других науках – появилось понятие радиана, представляющего собой 2π рад = 360° или, другими словами, 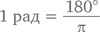
Для тауистов, почитающих число t как 2π, 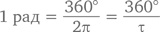
В числовом же выражении 1 радиан примерно равен 57°. Но зачем они нужны, спросите вы. И чем вдруг научному сообществу так не угодили привычные всем градусы? В круге с радиусом r угол в 2π радианов охватывает длину окружности 2πr. Если взять часть этого большого угла, величина дуги, отделяемой этой частью, будет в 2πr раз больше получившейся дроби. Если говорить конкретнее, то 1 радиан «захватывает» дугу длиной 2πr(1/2π) = r, а m радианов – дугу длиной mr. В единичной окружности значение угла в радианах равно длине соответствующей ему дуги. Разве не удобно? 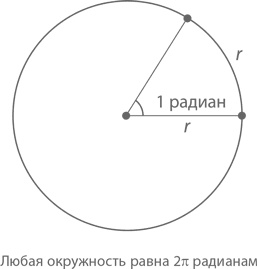
А вот единичный круг, поделенный на самые «популярные» углы – значения выражены как в градусах, так и в радианах. 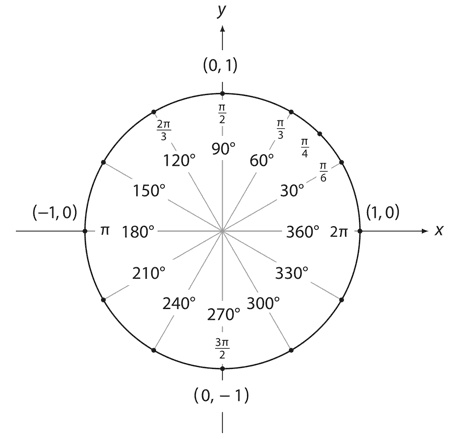
Для сравнения – версия с t вместо π. 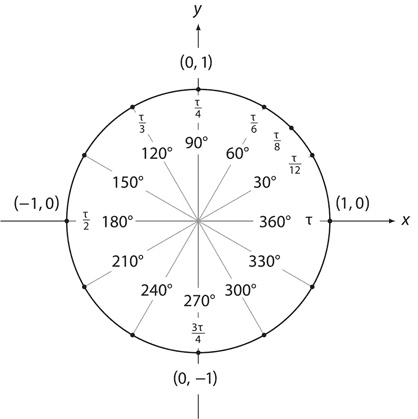
На рисунках, кстати, очень хорошо заметно, насколько t удобнее π. Для угла 90° (занимающего четверть окружности) представление в радианах выглядит как t/4; для угла 120° (треть окружности) – как t/3; для угла 60° (одна шестая окружности) – как t/6; t же есть, по сути, один полный оборот, то есть угол 360°. Как нам еще предстоит убедиться, радианы позволяют значительно упростить формулы и уравнения подсчета тригонометрических функций. Формулы синуса и косинуса, например, можно превратить в «бесконечные ряды многочленов»: sin x = x – x2/3! + x5/5! – x7/7! + x9/9! –… cos x =1 – x2/2! + x4/4! – x6/6! + x8/8! –… но только если x измеряется в радианах. Или при исчислении, например, мы увидим, что cos x есть производная функция sin x при том же условии. Так же и графики тригонометрических функций y = sin x и y = cos x строятся обычно на основании радианного представления x. 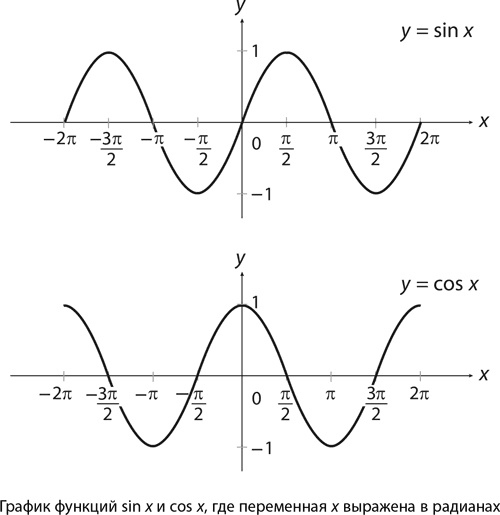
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно