Магия математики. Как найти x и зачем это нужно - читать онлайн книгу. Автор: Артур Бенджамин cтр.№ 55

Существует несколько забавных фактов, связанных с эллипсами, которыми я хотел бы с вами поделиться. Например, вы можете нарисовать овал с помощью двух канцелярских кнопок, лески и карандаша.

Возьмите кнопки, воткните их в лист бумаги или картона и накиньте на них колечко из лески или прочной нитки (но до предела не натягивайте). Поставьте карандаш кончиком в центр получившейся конструкции и оттяните один из концов лески так, чтобы получился треугольник. А теперь постепенно передвигайте карандаш по бумаге вокруг кнопок, не ослабляя леску. Диаграмма, получившаяся в результате, будет иметь эллиптическую форму.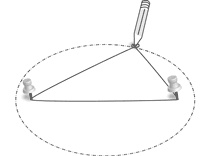

Местоположения кнопок называются фокусами эллипса, и они, конечно же, тоже волшебные. Если вместо кнопки в точку одного фокуса положить бильярдный шар и ударить по нему так, чтобы он покатился в случайном направлении, то после всего лишь одного касания о периметр он обязательно пройдет через точку второго фокуса.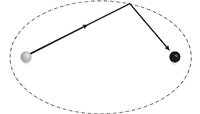

Кстати, космические тела, вроде планет и комет, путешествуют вокруг солнца именно по эллиптической орбите. Естественно, я не смог удержаться:

Число π появляется и в трехмерных фигурах. Возьмем для примера консервную банку, которая для любого математика является цилиндром. Так вот, объем цилиндра (то есть его внутреннее пространство) с радиусом r и высотой h составит

Объяснить эту формулу можно, представив цилиндр как совокупность окружностей, расположенных одна на другой так, чтобы образовалась стопка высотой h (представьте себе стопку подносов в ресторане и поймете, что я имею в виду).

А чему будет равна площадь поверхности цилиндра? Иными словами, сколько краски нам понадобится, чтобы покрасить все его внешние стороны, включая «крышку» и «донышко»? Держать ответ в памяти нет никакой необходимости – его можно получить в любой момент, условно разделив цилиндр на три части. Площади «крышки» и «донышка» будут равны πr². Значит, их общий вклад в площадь поверхности цилиндра составит 2πr². Чтобы узнать площадь третьей части, разрежем оставшийся «тубус» вдоль от верха до низа и разогнем его. У нас получится прямоугольник с шириной h и длиной 2πr (которая берется из длины прилегающей окружности). Его площадь будет равна 2πrh, что позволяет нам «собрать» формулу общей площади цилиндра:

Сфера есть трехмерный объект, в котором все наружные точки равноудалены от центра. Чему будет равен объем сферы с радиусом r? Начнем с того, что такого размера объект войдет в цилиндр, имеющий радиус r и высоту 2r, следовательно, его объем будет меньше πr²(2r) = 2πr³. По случайному стечению обстоятельств (надежно подкрепленному скрупулезными вычислениями) сфера займет ровно две трети этого пространства. Другими словами,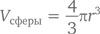

Формула для нахождения площади поверхности сферы выглядит еще проще, хотя путь к ней куда более тернист:

Давайте завершим раздел примерами, где у π появляется вкус мороженого и пиццы. Представьте себе рожок мороженого (также известный как конусовидный стаканчик) с высотой h и радиусом верхней окружности r. Длину образующей конуса – линии, проведенной от его кончика к любой точке верхней окружности – обозначим буквой s (самый простой способ ее вычислить – теорема Пифагора, потому что h² + r² = s²).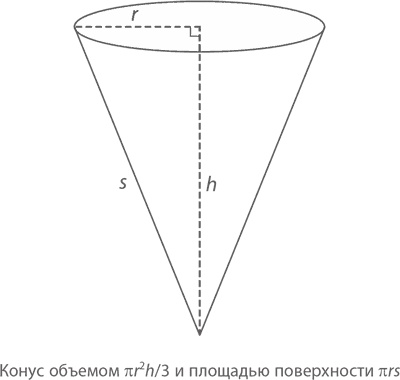

Конус этот легко уместится в цилиндр радиусом r и высотой h, поэтому неудивительно, что его объем будет меньше πr²h. Зато удивительно (и при этом очевидно без всяких вычислений) то, что меньше он будет ровно в 3 раза. Другими словами,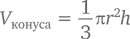

И хотя вычисления здесь и в самом деле совершенно не нужны, отказать себе в удовольствии, которое дарит нам эта красота и простота, совершенно невозможно: площадь поверхности конуса равна

Ну, и наконец, пицца, имеющая радиус z и толщину a, как видно на рисунке. Каков будет ее объем?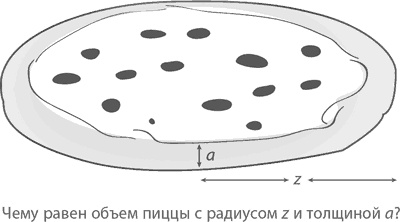

Это лакомство – не что иное, как необычной формы цилиндр (радиус z, высота a), объем которого равен

Немного переделаем эту формулу – уверен, у вас слюнки потекут:

В том, что число π появляется в площадях и длинах всех кругообразных объектов, рассмотренных нами, ничего удивительного нет. Но только этим сфера его влияния не ограничивается – оно обнаруживается даже там, где, казалось бы, ему делать совершенно нечего.