История лазера - читать онлайн книгу. Автор: Марио Бертолотти cтр.№ 50

В 1916 г., используя более тонкую модель эллиптических орбит, П. Дебай (1884—1966), нобелевский лауреат по химии 1936 г., и Зоммерфельд сумели дать объяснение нормальному эффекту Зеемана, однако аномальный эффект Зеемана все еще оставался загадкой. Эта проблема не была решенной, когда, примерно в 1920 г., Зоммерфельд предложил использовать эмпирическое объяснение, принимая во внимание экспериментальные данные. Он получал уровни энергий из частот наблюдаемых спектральных линий, находя затем квантовые числа, идентичные им. Это позволяло предсказать переходы с помощью подходящих правил отбора.

Следуя такой методологии, Зоммерфельд ввел новое квантовое число, которое он назвал внутренним квантовым числом. Позднее по предложению Бора его стали обозначать буквой j. Затем была разработана модель, названная векторной моделью, в которой число у представлялось суммой вектора углового момента электрона и углового момента остального атома, который создается ядром и остающимися электронами. Эти два момента складываются согласно сложным квантовым правилам.

Тем временем А. Ланде (1888—1975) стремился получать решение для аномального эффекта Зеемана, но привел ситуацию в непонятное состояние, когда он показал, что в некоторых случаях квантовые числа, связанные с магнитным поведением, могут иметь получисленные значения. Во всех этих, все еще непостижимых, исследованиях появилась идея, что орбита электрона обладает квантованным положением в пространстве. Таким образом, получила развитие идея пространственного квантования. Прямое подтверждение этому было дано в 1921 г. Отто Штерном (1888-1969) и Вальтером Герлахом (1889-1979).

Отго Штерн после получения докторской степени в университете Бреслау в 1912 г. последовал за Эйнштейном в Прагу (1912) и в Цюрих (1912—1914). В 1914 г. он стал приват-доцентом университета Франкфурт-на-Майне. Во время Первой мировой войны он был солдатом. Его назначали профессором разных немецких университетов, в конце концов, в Гамбурге. Возвратившись с войны во Франкфурт, он посвятил себя разработке метода молекулярных пучков. В этом методе, который требует получения очень высокого вакуума, получается пучок свободно летящих молекул или атомов. Наиболее важным требованием является проведение эксперимента в исключительно чистых условиях, подобных тем идеальным условиям, которые предполагаются в теории. Штерн и его сотрудники изучили основные положения, относящиеся к кинетической теории газов, доказали пространственное квантование, измерили магнитный момент протона, проверили соотношение де Бройля для волн атомов гелия и др.

Он покинул Германию в оппозиции к Гитлеру в 1933 г. и эмигрировал в США, где стал работать в Институте Технологии Карнеги в Питсбурге. Он получил Нобелевскую премию по физике за свои исследования молекулярных пучков.

Первой работой Штерна с молекулярными пучками было прямое подтверждение закона распределения по скоростям Максвелла и измерение средней скорости молекул.

Макс Борн (1882—1970), который был в университете Франкфурта в 1919 г. профессором теоретической физики, вспоминал, что он был так восхищен идеей такого измерения, что предоставил в распоряжение Штерна все возможности своей лаборатории, мастерских и механиков. Штерн был не очень умелым в работе руками, но он очень хорошо знал, как руководить техником, который мог сделать все. Позднее, в 1920 г., Вальтер Герлах, прекрасный экспериментатор, прибыл во Франкфурт, и Борн чрезвычайно обрадовался этой новости. Он воскликнул: «Слава Богу, теперь у нас есть, кто знает, как проводить эксперимент, давай, парень, помоги нам!» Вальтер Герлах получил докторскую степень по физике в университете Тюбингена в 1912 г. Во время службы в армии в Первой мировой войне он работал с Вильгельмом Вином над разработкой беспроволочной телеграфии. После короткого периода работы в промышленности он пришел во Франкфурт. Он уже имел дело с атомными пучками, когда работал в Тюбингене у Фридриха Пашена, и спроектировал эксперимент по изучению отклонения пучка атомов висмута в неоднородном магнитном поле с целью определения магнитных свойств.

Однажды Штерн пришел к нему и сказал: «С помощью магнитных экспериментов мы можем сделать еще кое-что. Знаешь ли ты, что существует направленное (пространственное) квантование?» «Нет, ничего не знаю» — ответил Герлах. В то время многие физики не верили, что пространственное квантование действительно существует, и полагали, что это лишь способ выполнения расчетов. Герлах позднее вспоминал, что Петер Дебай заметил ему: «Неужели вы верите, что пространственая ориентация имеет какой-либо физический смысл; это просто указание, как проводить вычисления». Даже Борн придерживался такого же мнения. Штерн, напротив, верил, что это реальный факт и после объяснения этого эффекта сказал Герлаху: «Это стоит попробовать» и предложил: «Почему бы нам не попробовать? Давай проверим это».

Оригинальное предложение Штерна было детально изложено в статье «Метод экспериментальной проверки квантования по направлению в магнитном поле».

Чтобы понять это утверждение, необходимо помнить, что уже А. М. Ампер (1775-1836), французский физик, который заложил математические основы электромагнетизма, установив связь между электричеством и магнетизмом, и который за свои таланты был назначен Наполеоном (1808 г.) генеральным инспектором новой системы университетов во Франции, продемонстрировал, что электрический ток в цепи генерирует небольшой магнитный момент, такой, как если бы эта цепь была элементарным магнитом. В атомах орбиты электронов, вращающихся вокруг ядер, могут уподобляться маленьким катушкам, через которые проходит ток. Квантовая механика Бора, улучшенная Зоммерфельдом, позволяет рассчитать магнитные моменты, связанные с каждой орбитой. Эти величины получаются по сложным правилам, найденным Зоммерфельдом. Таким образом, атомы обладают магнитным моментом и ведут себя подобно стрелке компаса, которая ориентируется во внешнем магнитном поле. Если атом помещен во внешнем магнитном поле, его момент, обозначаемый буквой l, будет выстраиваться параллельно внешнему полю согласно правилам электромагнетизма и классической механики. Чтобы сделать это, он будет описывать конус с осью вдоль направления поля (прецессионное движение). Его проекцию на направление поля (будем обозначать ее m) называют моментом вдоль поля (рис. 29).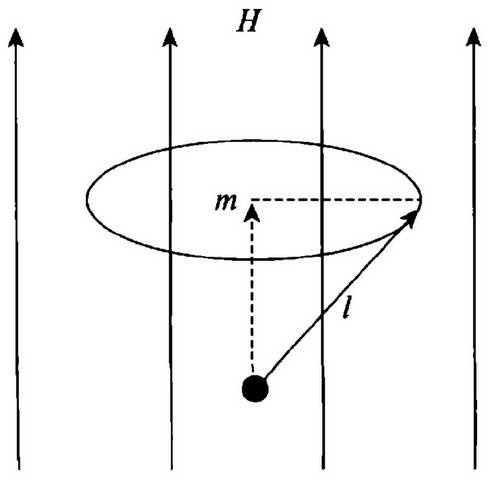

Рис. 29. Прецессия углового момента l в магнитном поле H. Показана проекция m вектора I на H

Теперь получается следующее. Согласно классической механике т компонента вдоль поля может иметь любое возможное значение между +l и —l (т.е. возможен любой угол между l и полем). Но согласно квантовой теории возможны лишь дискретные значения m, соответствующие m = l, (l — 1), (l — 2), ..., — l (т.е. разрешены лишь некоторые углы l по отношению к полю) (рис. 30). Согласно квантовой механике величина вектора l равна √(l +1), которая больше, чем максимальное значение m. Поэтому ясно, что l никогда не может точно направлено по полю (заключение, которое глубоко связано с принципом неопределенности Гейзенберга). Чтобы прояснить это для простейшего случая, когда магнитный момент атома (в соответствующих единицах измерения) l = 1/2, вообразим, что магнитное поле направлено снизу вверх, как показано на рис. 31, а атом является человеком, держащим стрелу (которая и есть на нашем рисунке магнитным моментом). В то время, как согласно классическим законам, человек может ориентировать стрелу в любом направлении, согласно квантовой механике позволены только две позиции, показанные на рисунке (мы будем называть их параллельной и антипараллельной ориентацией по отношению к полю), в которых проекция стрелы на направление поля есть либо + 1/2, либо — 1/2 (рис. 31, а). Поэтому длина стрелы √(3/2).