
|
||
|
|
||
|
|
Онлайн книга - История лазера | Автор книги - Марио Бертолотти
Cтраница 21

Первыми интересами Стрэтта были акустика и физиология слуха. В этих областях он проявил свои научные способности, о чем свидетельствует его книга «Теория звука», опубликованная в 1877 г. и все еще не утратившая своей значимости. В 1871 г. он женился на Эвелин Бальфур, сестре своего приятеля по колледжу, и поселился в семейном поместье в Терлинге (около 70 км к северо-востоку от Лондона), где организовал свою лабораторию. Здесь он начал серию экспериментальных исследований в области акустики и оптики. С детства интересуясь фотографией, он описал технику цветной фотографии (1887 г.), которая позднее в 1891 г. была реализована Г. Липпманом (1845—1921), который в 1908 г. получил Нобелевскую премию по физике за «его метод фотографического воспроизведения цветов, основанного на явлении интерференции». Изучая дифракционные решетки, Стрэтт ввел свой знаменитый критерий разрешающей силы, который сегодня известен как критерий Рэлея. Проводя свои ранние эксперименты по цветному зрению, он пришел к изучению голубого цвета неба, и правильно связал это с рассеянием света молекулами воздуха и получил количественное соотношение, описывающее это. Вплоть до второй половины XIX в. в университетах не было учебных лабораторий для обучения «практической физикой» в пределах университетских курсов. Великие экспериментаторы обучались экспериментальной технике в частных лабораториях или при помощи старших мастеров этого дела. В 1850 г. Вильям Томсон (лорд Кельвин) освободил старый винный подвал в колледже г. Глазго и устроил там студенческую лабораторию для исследований электричества. Были устроены и другие лаборатории, и в 1869 г. комитет Кембриджа рекомендовал установить специальную профессуру для обучения и демонстраций экспериментальной физики. В следующем году ректор университета, седьмой герцог Девонширский (Вильям Кавендиш), поддержал организацию исследовательской лаборатории. Ею стала Кавендишская лаборатория, главой которой был Максвелл, вплоть до своей смерти в 1879 г. В декабре 1879 г. лорд Рэлей был приглашен занять эту должность, и когда он ушел в отставку и удалился в Терлинг в 1884 г., это место занял его ученик Дж. Дж. Томсон. В 1896 г. Рэлей стал секретарем Королевского Общества, а в 1897 г. заменил Джона Тиндаля на посту Профессора Натуральной Философии в Королевском Институте и занимал этот пост до 1905 г. К этому периоду относится открытие вместе с Вильямом Рамзеем (1852— 1916) из Лондонского университета газа аргона, за что в 1904 г. Рэлей получил Нобелевскую премию по физике, а Рамзей — Нобелевскую премию по химии. Годы с 1895 до 1919 были годами почета и славы. В 1899 г. Рэлей заинтересовался проблемой черного тела. Здесь стоит более детально обсудить подходы Рэлея, поскольку некоторые концепции будут нам полезны в дальнейшем. Кинетическая теория тепла, принципиально разработанная Людвигом Больцманом, Джеймсом Клерком Максвеллом и Джошуа Виллардом Гиббсом, рассматривала тепло как результат беспорядочного движения многих атомов и молекул, из которых состоят все тела. Поскольку попытки проследить движение отдельного атома или молекул бесполезны, математическое описание тепловых процессов с необходимостью основано на статистических методах. Чтобы объяснить макроскопические характеристики, например, газа, рассматриваются усредненные величины, определяемые большим числом молекул. Одним из фундаментальных принципов такого метода является т.н. теорема равновесности, математически выведенная Максвеллом на основе ньютоновых принципов механики. Эта теорема гласит, что «полная энергия, заключенная в системе большого числа частиц, которые обмениваются энергией за счет беспорядочных столкновений, равномерно распределена (в среднем) по всем частицам». Если, например, Е — полная энергия, a N— число частиц, то усредненная энергия частицы — E/N. Хотя принцип равновесности регулирует распределение энергии среди большого числа частиц, скорость и энергия индивидуальной частицы могут отличаться от среднего значения, статистически флуктуируя около этого значения. Это означает, что если средняя энергия имеет определенное значение, то некоторые молекулы могут иметь большие энергии, а некоторые меньшие. Эти различающиеся величины называются флуктуациями. Если мы математически представим эти флуктуации, например скорость молекул в газе, то получим кривые, которые показывают относительное число частиц, имеющих определенную скорость для каждой температуры, скорости большие или меньшие, чем среднее значение. Эти кривые, впервые выведенные Максвеллом и носящие его имя, представлены на рис. 14 для трех различных температур газа. 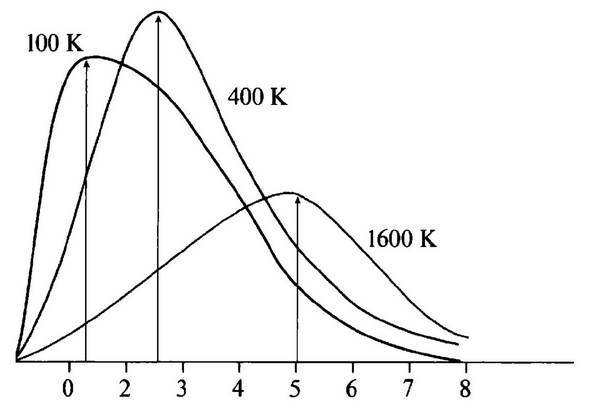
Рис. 14. Распределение Максвелла: число молекул с данной скоростью дается как функция скорости для трех различных значений температуры: 100, 400 и 1600 К. Так как число молекул в сосуде не изменяется, площади под этими тремя кривыми равны. Средняя скорость молекул (показана стрелками) увеличивается пропорционально квадратному корню из абсолютной температуры Использование статистического метода для изучения теплового движения молекул очень хорошо объясняет термические свойства материальных тел, особенно в случае газов. Идея лорда Рэлея была распространить статистический метод и на тепловое излучение. При исследовании распределения интенсивности света, испускаемого на разных частотах, как функции температуры, получаются кривые, как показано на рис. 13, на котором представлены распределения для четырех разных температур. Эти кривые при сравнении с теми, которые показаны на рис. 14, обнаруживают заметное сходство: на рис. 14 увеличение температуры сдвигает максимум кривой в сторону больших скоростей, а на рис. 13 максимум сдвигается в сторону больших частот излучения. Этот факт побудил Рэлея применить к тепловому излучению тот же принцип равновесности, который столь плодотворен в случае газа, т.е. предположить, что полная энергия излучения равномерно распределена среди всех возможных колебательных частот (т.н. мод). Это представляется вполне корректным с классической точки зрения. Рэлей, однако, совершил небольшую ошибку в подсчете числа мод, которую позднее в 1906 г. поправил физик, астроном и математик Джеймс Джине (1877—1946), так что сегодня эта формула известна как закон Рэлея—Джинса. На больших длинах волн эта формула очень хорошо объясняла экспериментальные результаты. Однако она оказывалась непригодной на коротких длинах волн, давая странные результаты. Неприятность заключалась в том, что, несмотря на все сходство между газом, состоящим из отдельных молекул, и теплового излучения, состоящим из электромагнитных колебаний, имеется существенное различие. В то время как число молекул газа в замкнутом объеме всегда конечно, даже если оно весьма велико, число возможных электромагнитных колебаний (мод) в таком же замкнутом объеме всегда бесконечно. 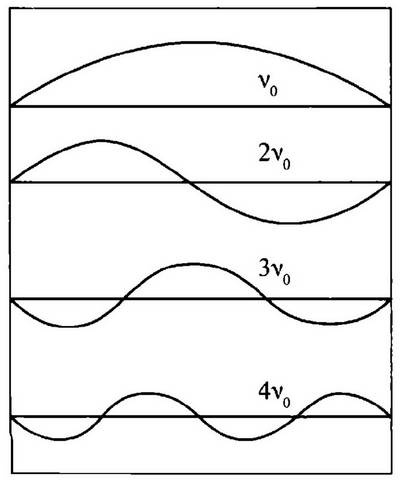
Рис. 15. Колебания струны. На верхней части показано основное колебание, а при движении вниз — последовательные его гармоники Чтобы понять этот факт, мы можем рассмотреть простой случай волнового движения в одном направлении (одномерный случай), представляемого движением струны, закрепленной на концах. Поскольку концы струны не могут двигаться, единственными возможными являются колебания, показанные на рис. 15, которые на музыкальном языке соответствуют основной ноте и различным гармоникам (обертонам): на длине струны могут существовать полволны, две полуволны, три, десять, тысяча и любое целое число полуволн. Соответствующие частоты колебаний в два, три, десять, тысячу раз больше, чем частота основной ноты. В случае стационарных волн в трехмерной коробке (полости), например, в кубе ситуация такая же, хотя и немного сложнее, но результат тот же в том смысле, что имеется неограниченное число разных колебаний, с длинами волн все короче, и с соответствующими частотами все выше. Если мы примем принцип равновесности и будем считать, что Е — полная энергия, заключенная в полости, тогда эта энергия, деленная на полное число мод, будет соответствовать энергии одиночного колебания и, поскольку число мод бесконечно, эта энергия должна быть бесконечно малой величиной! Это заключение совершенно абсурдно, и даже невероятно, если мы приложим его к черному телу Кирхгофа. Если мы позволим некоторому, малой величины, излучению на некоторой длине волны, например красной, попасть в полость, то оно там начнет взаимодействовать со стенками и будет распределено среди бесконечных колебательных мод, содержащихся в полости, т.е. среди бесконечного числа частот, простирающихся ниже, чем красная, и выше, чем красная, т.е. в области ультрафиолетового излучения, рентгеновского, γ-лучей и т.д. Этот парадоксальный результат был назван «ультрафиолетовой катастрофой». Согласно этому анализу, открытая дверца печи на кухне должна была бы быть источником рентгеновских и γ-лучей, подобно атомной бомбе!
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно