Солнечная система - читать онлайн книгу. Автор: Алексей Бережной, Владимир Сурдин cтр.№ 7

υ_p=υ_I(a)√(1+e)/√(1—e) и υ_a=υ_I(a)√(1—e)/√(1+e)

Здесь υ_I(a) — круговая скорость на расстоянии от a до S. В свою очередь υ_I убывает обратно пропорционально квадратному корню из расстояния до S: υ_I=K/√r.

Между большой полуосью и периодом обращения существует связь, открытая еще И. Кеплером в начале XVII в.:

Р = 2π(а^3/2/K) (5)

Разумеется, выражение постоянной К через G и М — заслуга Ньютона.

Если эллипс близок к окружности, различие скоростей в разных точках орбиты невелико. У Земли в ее движении вокруг Солнца е=0,016, υ_p=31км/с, υ_a=29км/с. У кометы Галлея эллипс очень вытянут: е=0,96; так что υ_p=51км/с, υ_a=1км/с. Такой характер ускорений и замедлений на орбите понять легко, если воспользоваться аналогией с вращением грузика на стержне вокруг горизонтальной оси. Внизу скорость наибольшая, наверху — наименьшая. В нашей задаче «вниз» — это направление к притягивающему центру, «вверх» — прочь от него. Причина изменений скорости и для планеты, и для маятника одна: закон сохранения энергии. «Наверху» потенциальная энергия гравитации максимальна, «внизу» — минимальна. Для кинетической энергии соотношение противоположно.

Набор орбит оказался небольшим. В век космонавтики мы можем выбирать высоту или период обращения искусственных небесных тел в широких пределах, но в силу (5) по отдельности, а не вместе. Наименьший период обращения ИСЗ — полтора часа — соответствует круговой орбите минимальной высоты. Максимального периода теоретически нет, но подавляющее большинство ИСЗ имеют период не более 24 час.

Притяжение и форма небесных тел

Многие искусственные спутники Земли (ИСЗ) летают низко, почти царапая Землю: в масштабе школьного глобуса (1:50000000) не далее сантиметра от него. Тут уж даже Землю шаром считать нельзя, хоть на глазок это и незаметно. А вот Юпитер и особенно Сатурн обладают отчетливо видимым сжатием. Одним словом, чтобы идти дальше, надо разобраться с формой небесных тел и их притяжением.

Начнем с последнего. Пусть нам известна форма и строение протяженного небесного тела Т. Как определить силу тяготения, с которой Т притягивает какую-либо частицу Q? Перейдем к ускорению — оно не зависит от массы пробной частицы (уникальное свойство гравитационного поля, открытое Г. Галилеем). Поэтому можно считать, что Т создает вокруг себя (и в себе самом тоже) поле ускорений, математически точное описание гравитационного поля. Как найти его? Разобьем мысленно Т на столь малые кубики, чтобы их размерами можно было бы пренебречь по сравнению с расстоянием до Q (рис.5).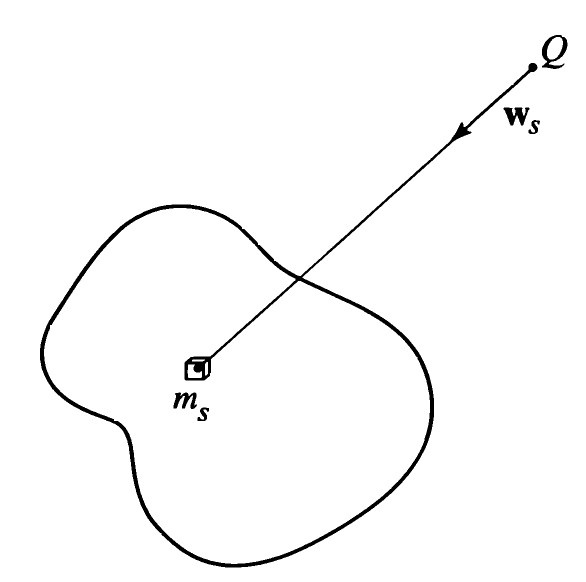

Рис.5

Вектор ускорения w_s, сообщаемого Q со стороны s-гo кубика, равен согласно (1)

w_s=—(Gm_s/r_s³)r_s (6)

Поясним, откуда взялся минус и куб в знаменателе. Модуль ускорения равен Gm_s/r_s², и он умножен на единичный вектор —r_s/r_s направления от массы m_s к точке Q (рис.5). Полное ускорение равно векторной сумме (6) по всем кубикам. Разумеется, так получается приближенная величина. Чтобы вычислить точную, нужно перейти к пределу, устремляя ребро кубика к нулю. В пределе получим тройной интеграл по телу Т. С помощью хорошего компьютера интеграл взять нетрудно. Но ведь даже для данного тела его нужно считать в огромном количестве точек пространства. Чаще всего идут другим путем. Как уже говорилось, Ньютон сумел вычислить интеграл для шара со сферическим распределением плотности и убедился, что внешние частицы шара притягивают в точности как материальная точка той же массы, помещенная в его центре. А дальше П.-С. Лаплас предложил следующую схему определения гравитационного поля Т. Во-первых, проще вместо векторного поля ускорений иметь дело со скалярным полем гравитационной потенциальной энергии Е_р единицы массы Q. Оба поля однозначно определяют друг друга. Во-вторых, представим поле в виде ряда, т.е. суммы бесконечного числа слагаемых:

Е_р=V₀+V₁+V₂+… (7)

Здесь начальное слагаемое описывает притяжение шара с центром в центре масс Т и нам уже известно из формулы (4): V₀=—К²/r. В отличие от силы, потенциал шара убывает обратно пропорционально первой степени расстояния от центра масс Т. Следующие слагаемые V_s убывают обратно пропорционально r^s+1, причем V₁=0. Если Q далеко, то достаточно взять несколько первых членов (7) или даже только начальный член, чтобы получить удовлетворительную точность. Иными словами, гравитационное поле любого тела с удалением от него все больше напоминает поле шара, в полном соответствии с наблюдением древних софистов, что издали и квадратная башня кажется круглой. Для близких Q (например, если Т — Земля, Q — ИСЗ) для высокоточного определения гравитации надо брать десятки и сотни слагаемых. Каждое из них представляет не очень сложную функцию координат точки Q. Например,

V₂=(A₁x²+A₂y²—(A1+A2)z²+A₃xy+A₄yz+A₅zx)/r⁵

Важно, что V_s содержит числовые коэффициенты. Например, в V₂ их пять: A₁÷А₅. Эти коэффициенты можно определить, измеряя гравитационный потенциал, или ускорение на поверхности тела или вблизи нее. А можно следить за движением его искусственных спутников. В любом случае мы получаем систему многих алгебраических уравнений со многими неизвестными (коэффициентами типа A_s). Ее решение непросто, но современная математика и вычислительная техника с этим справляется.

Итак, мы описали два способа представления гравитационного поля любого тела: тройным интегралом и рядом Лапласа. Существует еще несколько способов, и в каждой конкретной задаче можно выбрать оптимальный.

Перейдем к вопросу о форме, которую придает гравитация небесному телу. Пусть выполнены следующие три допущения. Во-первых, тело изолировано и компактно, т.е. никакие другие тела на него не действуют, а самогравитация значительна. Во-вторых, тело находится в жидком, газообразном или пластическом состоянии. В третьих, в теле нет источников энергии. Насколько реальны эти допущения?

1. Полной изолированности, конечно, нет. В качестве примера сравним силы, с которыми притягивают каждого из нас Земля (F₁) и Луна (F₂). В подлунной точке (там, где Луна видна в зените) в момент, когда Луна в перигее своей орбиты, F₂ максимальна. Но и тогда F₂/F₁≈4×10^-6. На самом деле влияние Луны на форму Земли еще меньше. Именно оно вызывает приливы, о чем еще будет рассказано. Сейчас достаточно заметить, что изолированность в Солнечной системе выдержана в очень хорошем приближении.