Рассказ предка. Паломничество к истокам жизни - читать онлайн книгу. Автор: Ричард Докинз cтр.№ 23

Теперь возьмем много кусочков сахара разного размера и построим диаграмму, где на горизонтальной оси отложена масса (она пропорциональна объему), а на вертикальной – начальная скорость растворения кусочка (которую мы полагаем пропорциональной площади). На нелогарифмическом графике точки расположены вдоль кривой. Эту линию трудно интерпретировать. Но если мы отложим на графике логарифм массы и логарифм начальной скорости растворения, картина получится информативнее. На каждое троекратное увеличение логарифма массы будет приходиться двукратное увеличение логарифма площади поверхности. В логарифмическом масштабе точки не расположены вдоль кривой: они распределятся вдоль прямой линии. Более того, угол наклона этой прямой составит два к трем, то есть на каждые два шага по оси площади будет приходиться три шага по оси объема. На каждое двукратное увеличение логарифма площади будет приходиться троекратное увеличение логарифма объема. Угол наклона прямой на двойном логарифмическом графике может быть и другим. Графики подобного рода наглядны, потому что угол наклона прямой позволяет почувствовать, как взаимодействуют объем и площадь. А объем, площадь и сложные отношения между ними чрезвычайно важны для понимания того, как устроены организмы и их части.

Я не так уж силен в математике, но и меня очаровали эти расчеты. Еще сильнее меня восхищает, что этот же принцип годится для любых других фигур – не обязательно куба и сферы, но и для сложных: животных и органов животных, например почек и мозга. Для этого нужно, чтобы изменение размера представляло собой пропорциональное увеличение или уменьшение без изменения формы. Это дает нечто вроде нулевой гипотезы, исходя из которой мы можем оценивать реальные размеры. Так, если тело одного животного десятикратно длиннее тела второго, то его масса будет больше в тысячу раз, но лишь при условии, что у них одинаковая форма. Однако форма тела, судя по всему, закономерно эволюционировала по мере движения от маленьких животных к большим, и сейчас мы увидим, почему.

Форма тела крупных и мелких животных неизбежно различается – хотя бы из-за соотношения площади и объема. Если бы мы сделали из землеройки слона, пропорционально ее увеличив и сохранив форму, она бы не выжила. Она стала бы в миллион раз тяжелее, а это породило бы множество проблем. Одни связаны с объемом (массой). Другие – с площадью поверхности. Третьи – с соотношением этих двух величин или другими факторами. Точно так же, как скорость растворения куска сахара зависит от площади его поверхности, у животного скорость теплоотдачи или испарения воды через кожу пропорциональна площади поверхности его тела. Однако скорость теплопродукции, судя по всему, сильнее зависит от числа клеток, которое, в свою очередь, является функцией от объема.

Землеройка размером со слона сохранила бы веретенообразные ножки, которые быстро подломились бы. Ее мышцы были бы слишком тонкими, ведь сила мышцы пропорциональна не ее объему, а площади поперечного сечения. Мышечное движение – суммарное движение миллионов крошечных волокон. Число волокон, которые можно “упаковать” в мышцу, зависит от площади ее поперечного сечения (линейный размер в квадрате). Но работа, которую должна выполнять мышца – например поддержка слона, – пропорциональна массе слона (линейный размер в кубе). Поэтому слону для поддержания тела необходимо пропорционально больше мышечных волокон, чем землеройке. Соответственно, поперечное сечение мышц слона должно быть большим, чем можно ожидать при простом увеличении масштаба. То же касается объема мышц. По разным причинам это правило относится и к костям. Именно поэтому у слонов и других крупных животных ноги толстые, как стволы деревьев.

Допустим, что животное размером со слона стократно крупнее землеройки. Если форма тела у них одинакова, то площадь поверхности кожи первого животного будет в 10 тыс. раз больше, чем у землеройки, а объем и масса тела – в миллион раз больше. И если сенсорные клетки будут распределены на коже таким же образом, у слона их будет в 10 тыс. раз больше – а значит, обслуживающая их область мозга должна пропорционально увеличиться. Всего у первого животного в миллион раз больше клеток, чем у землеройки, и ко всем им должны подходить капилляры. Сколько километров кровеносных сосудов у крупного животного? Посчитать это довольно сложно, мы займемся этим после. Пока достаточно понимания, что в подобных случаях всегда нужно учитывать правила соотношения объема и площади поверхности. И логарифмический график – это отличный способ интуитивного понимания таких вещей. Основной вывод таков: по мере того, как животные в процессе эволюции становятся крупнее или мельче, форма их тела предсказуемо изменяется.

К этому нас привели размышления о размере мозга. Нельзя сравнивать наш мозг с мозгом H. habilis, Australopithecus или любого другого вида, не делая поправку на размер тела. Для этого нам нужен некий индекс размера мозга, учитывающий поправку на размер тела. Причем мы не можем просто разделить размер мозга на размер тела, хотя уже это было бы лучше сравнения абсолютных размеров мозга. Лучший способ – это использование логарифмических графиков. Нужно построить на графике зависимость логарифма массы мозга от логарифма массы тела для животных разного размера. Отметки, скорее всего, будут располагаться на прямой – примерно так, как на графике выше. Если угол наклона прямой составит 1/1 (то есть размер мозга строго пропорционален размеру тела), это означает, что каждая клетка мозга может обслуживать определенное число клеток тела. Угол наклона 2/3 говорил бы, что мозг подобен костям и мышцам: для определенного объема тела (или количества клеток тела) необходима определенная площадь поверхности мозга. Так каков же угол наклона этой прямой?

Он находится примерно между 1/1 и 2/3. Лучше всего он соответствует 3/4. Почему? Это отдельная история, которую расскажет цветная капуста. (Мозг немного похож на цветную капусту, не так ли?)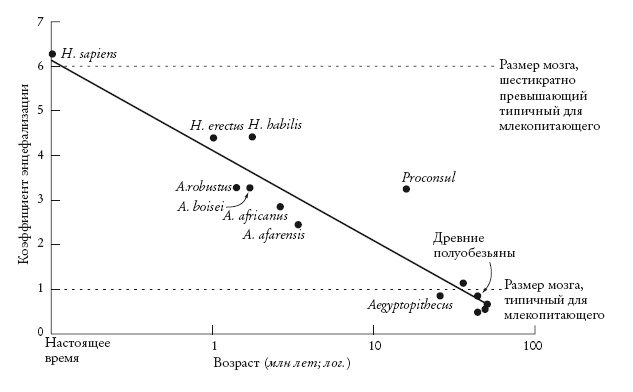

График изменения во времени коэффициента энцефализации (EQ) для различных ископаемых. Время в миллионах лет отложено по логарифмической шкале. Результаты представлены с поправкой на угол наклона 3/4.

Но пока я скажу лишь, что угол наклона 3/4 характерен не только для мозга, но возникает у всех видов живых существ, включая растения – например цветную капусту. В “Рассказе Цветной капусты” мы ознакомимся с интуитивно понятным объяснением этого факта. Что касается размера мозга, то именно 3/4 мы будем использовать, говоря о “прогнозируемом” соотношении, о котором шла речь выше.

Хотя точки на графике группируются вокруг “прогнозируемой” прямой с углом наклона 3/4, с ней совпадают не все точки. Если точка на графике лежит выше прямой, можно сказать, что у животного “большой” мозг – то есть он крупнее, чем “прогнозируемый” при данном размере тела. Животные, у которых мозг меньше “прогнозируемого”, располагаются ниже прямой. Расстояние от точки до прямой говорит о том, насколько мозг животного больше или меньше “прогнозируемого”. Так, точка, лежащая непосредственно на прямой, обозначает животное, размер мозга которого точно равен прогнозируемому.