Мир в ореховой скорлупке - читать онлайн книгу. Автор: Стивен Хокинг cтр.№ 20

В 20-х числах Сатурн перемещается в область вашей солнечной карты, связанную с обязательствами и карьерой, и вам предстоит научиться брать на себя ответственность и иметь дело со сложными отношениями. Однако в период полнолуния вы получите удивительное откровение и сможете охватить взглядом всю вашу жизнь, и это вас преобразит.

Однако действительная причина, по которой ученые не верят в астрологию, связана не с научными фактами или их отсутствием, а с тем, что астрология несовместима с другими теориями, которые были проверены в экспериментах. Когда Коперник и Галилей открыли, что планеты обращаются вокруг Солнца, а не вокруг Земли, а Ньютон открыл законы, которые управляют их движением, астрология стала крайне неправдоподобной. С чего бы положение других планет на фоне далеких звезд, каким оно видится с Земли, могло коррелировать с макромолекулами на небольшой планете, которые называют себя разумной жизнью (рис. 4.1)? А ведь это именно то, в чем астрология хотела бы нас убедить. Некоторые теории, описанные в этой книге, имеют не больше экспериментальных подтверждений, чем астрология, но мы верим в них, поскольку они совместимы с теориями, которые выдержали проверку Успех законов Ньютона и других физических теорий привел к идее научного детерминизма, которую впервые высказал в начале XIX века французский ученый маркиз де Лаплас. Он предположил, что если мы узнаем положения и скорости всех частиц во Вселенной в один момент времени, то законы физики должны позволить нам предсказать состояние Вселенной в любой другой момент времени в прошлом и в будущем (рис. 4.2).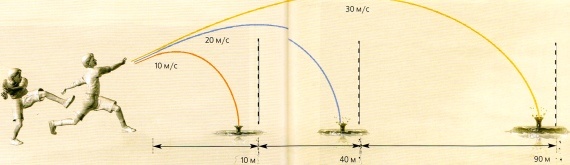

Рис. 4.2

Зная, с какой скоростью брошен бейсбольный мяч, вы можете предсказать, сколько он пролетит.

Другими словами, если научный детерминизм верен, мы, в принципе, могли бы предсказывать будущее и не нуждались бы в астрологии. Конечно, на практике даже такие простые уравнения, как те, что вытекают из ньютоновской теории тяготения, невозможно решить точно более чем для двух частиц. К тому же уравнения часто обладают свойством, называемым хаотичностью, из-за которого небольшое изменение положения или скорости в один момент времени приводит к совершенно иному поведению системы спустя некоторое время. Как знают те, кто смотрел «Парк юрского периода», крошечное возмущение в одном месте может повлечь за собой большие перемены в другом. Бабочка, взмахнувшая крыльями в Токио, способна вызвать дождь в Центральном парке Нью-Йорка (рис. 4.3).

Проблема в том, что последовательность событий невоспроизводима. В следующий раз, когда бабочка взмахнет крыльями, огромное множество других факторов окажутся иными, и они тоже будут влиять на погоду. Вот почему прогнозы синоптиков столь ненадежны.

По той же причине мы не достигли больших успехов в предсказании человеческого поведения на основе математических уравнений, хотя законы квантовой электродинамики должны, в принципе, позволять нам вычислить всё в химии и биологии. Тем не менее, несмотря на практические трудности, большинство ученых успокаивает себя мыслью, что — опять же в принципе — будущее все-таки предсказуемо.

На первый взгляд детерминизм должен был быть подорван принципом неопределенности, который говорит, что мы не можем одновременно точно измерить и положение, и скорость частицы. Чем точнее мы измеряем положение, тем менее точно определяется ее скорость, и наоборот. Лапласовская версия детерминизма утверждает что если мы знаем положения и скорости частиц в момент времени, то можем определить их положение в любой момент в прошлом и в будущем. Но как приступить к этому делу, если принцип неопределенности мешает точно узнать положения и скорости в один и тот же момент времени? Как бы ни был хорош наш компьютер, если мы вводим неточные данные, то получим неточные предсказания.

Однако детерминизм был восстановлен в модифицированной форме новой теорией, называемой квантовой механикой, которая включает в себя принцип неопределенности. Упрощенно говоря, квантовая механика позволяет точно предсказать половину того, что было возможно согласно классической лапласовской точке зрения. У частицы в квантовой механике нет точно определенных положения и скорости, но ее состояние можно описать так называемой волновой функцией (рис. 4.4).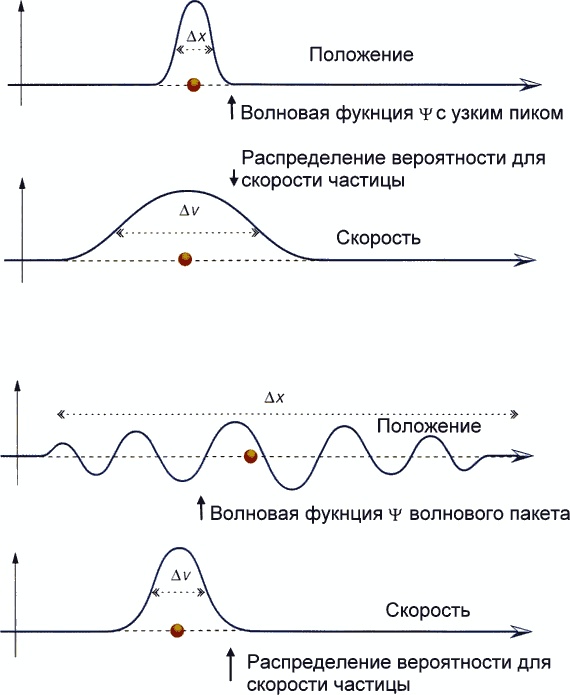

Рис. 4.4

Волновая функция определяет вероятности того, что частица будет иметь разные положения и скорости, таким образом, что Ах и Av удовлетворяют принципу неопределенности.

Волновая функция — это числовое значение в каждой точке пространства, которое дает вероятность того, что частица обнаружится в данном месте. Быстрота, с которой волновая функция изменяется от точки к точке, говорит нам о том, насколько вероятны различные скорости частицы. Некоторые волновые функции имеют четкий пик в определенной точке пространства. В таких случаях существует лишь небольшая неопределенность в положении частицы. Но из диаграммы видно, что в этом случае волновая функция быстро меняется в окрестности данной точки — поднимается с одной стороны и падает с другой. Это означает, что распределение вероятности для скорости является очень широким. Иными словами, велика неопределенность скорости. Рассмотрим, с другой стороны, непрерывную череду идущих друг за другом волн. Теперь велика неопределенность положения, но мала неопределенность скорости. Так что описание частицы при помощи волновой функции не имеет хорошо определенного положения или скорости. Оно удовлетворяет принципу неопределенности. Теперь понятно, что волновая функция — это все, что поддается точному определению. Мы не можем даже предположить, что частица имеет положение и скорость, которые известны Богу, но скрыты от нас. Подобные теории со «скрытыми переменными» дают предсказания, которые не согласуются с наблюдениями. Даже Бог ограничен принципом неопределенности и не может знать сразу и положения, и скорости — только волновую функцию.

Скорость, с которой волновая функция изменяется во времени, задается так называемым уравнением Шрёдингера (рис 4.5).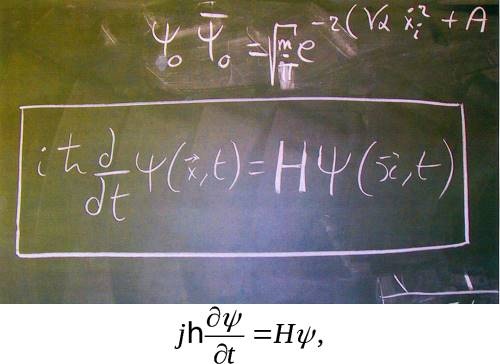

Рис. 4.5 Уравнение Шредингера

Эволюция во времени волновой функции Ψ определяется оператором Гамильтона Н, который связан с энергией рассматриваемой системы.

Зная волновую функцию в один момент времени, можно использовать уравнение Шрёдингера, чтобы вычислить ее в любой другой момент — прошлый или будущий. Таким образом, детерминизм сохраняется в квантовой теории, но в меньшем объеме. Вместо того чтобы предсказать сразу и положение, и скорость, мы можем предсказать только волновую функцию. Это позволяет нам точно предсказывать либо положения, либо скорости, но не то и другое. Так что в квантовой теории возможность делать точные предсказания ровно вдвое меньше, чем в классической лапласовской картине мира. Тем не менее в этом ограниченном смысле можно по-прежнему утверждать, что детерминизм в ней сохраняется.