Мир в ореховой скорлупке - читать онлайн книгу. Автор: Стивен Хокинг cтр.№ 11

Если струны обладают грассмановскими измерениями наряду с обычными, их колебания будут соответствовать бозонам и фермионам. В этом случае положительные и отрицательные энергии основных состояний в точности сокращаются, так что не остается никаких бесконечностей, даже малого порядка. Суперструны, как было объявлено, представляют собой Теорию Всею.

Историкам науки в будущем наверняка будет интересно построить график колебания пристрастий физиков-теоретиков. Струны безраздельно властвовали несколько лет, а супергравитация была низведена до статуса приближенной теории, годной при низких энергиях. Ярлык «низких энергий» был просто убийственным, несмотря даже на то, что в данном контексте низкоэнергетическими считались частицы, в миллиард миллиардов раз превосходящие по энергии те, что образуются при взрыве тротила. Будь супергравитация низкоэнергетическим приближением, ее нельзя было бы считать фундаментальной теорией Вселенной. Вместо нее на эту роль претендовали целых пять различных теорий суперструн. Но какая же именно из этих пяти струнных теорий описывает нашу Вселенную? И как можно построить теорию струн за пределами того приближения, в котором струны представляются поверхностями с одним пространственным и одним временным измерением в плоском пространстве-времени? Не могут ли струны искривлять фон пространства-времени?

В следующие за 1985-м годы постепенно становилось ясно, что теория струн не дает законченной картины. Начать с того, что струны, как выяснилось, лишь один из элементов широкого класса объектов, которые могут иметь более одного измерения. Пол Таунсенд, который является, как и я, сотрудником факультета прикладной математики и теоретической физики Кембриджа и по большей части заложил основу для изучения таких объектов, стал называть их «р-бранами». Такая р-брана имеет протяженность в р направлениях. Так, при р = 1 брана является струной, при р = 2 — поверхностью или мембраной и т. д. (рис. 2.15).

Рис. 2.15. Р-браны

Р-браны — это объекты, протяженные в р измерениях. Частными их случаями являются струны, для которых р = 1, и мембраны (р = 2), но в 10- или 11-мерном пространстве-времени возможны и большие значения р. Часто некоторые или все из р измерений свернуты наподобие тора.

По-видимому, нет причин отдавать предпочтение струнам с р = 1 перед струнами с другими значениями р. Напротив, следует принять принцип р-бранной демократии: все р-браны созданы равными ^[8].

Все р-браны можно найти как решения уравнений теории супергравитации в 10 или 11 измерениях. Хотя 10 или 11 измерений, кажется, не слишком похожи на знакомое нам пространство-время, идея состоит в том, что дополнительные 6 или 7 измерений свернуты до такой малой величины, что мы их не замечаем; нам видны только остальные 4 больших и почти плоских измерения.

Должен сказать, что я с неохотой принимаю идею дополнительных измерений. Но для меня, как для позитивиста, вопрос «Существуют ли дополнительные измерения на самом деле?» не имеет смысла. Все, о чем можно спросить: действительно ли математическая модель с дополнительными измерениями хорошо описывает Вселенную? У нас пока нет наблюдений, объяснение которых требовало бы дополнительных измерений. Однако есть вероятность, что они могут появиться на Большом адронном коллайдере LHC в Женеве. Но вот что заставляет многих людей, включая меня, всерьез принимать модели с дополнительными измерениями: это наличие между этими моделями целой сети неожиданных соотношений, называемых дуальностями. Данные соотношения показывают, что все модели, по сути, являются эквивалентными, они лишь отражают разные аспекты одной и той же лежащей в основе теории, которую назвали М-теорией. Не воспринимать эту сеть дуальностей как знак того, что мы находимся на верном пути, было бы все равно что верить, будто Бог поместил среди камней ископаемые остатки, чтобы запутать Дарвина в вопросе об эволюции жизни.

Дуальности показывают, что все пять теорий суперструн описывают одну и ту же физическую реальность и что они к тому же эквивалентны супергравитации (рис. 2.16).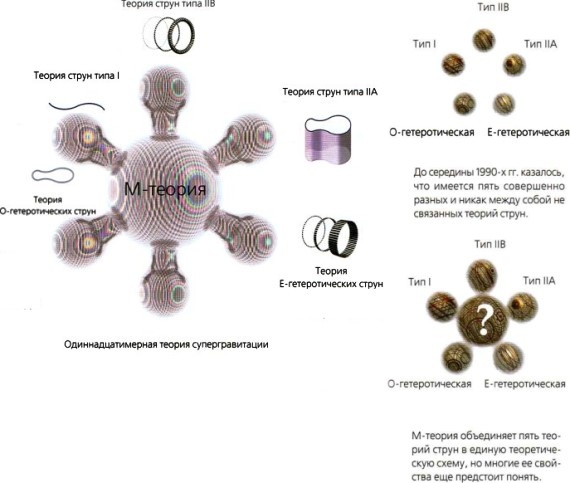

Рис. 2.16

Существует сеть взаимосвязей, так называемых дуальностей, которые соединяют все пять теорий струн, а также 11-мерную супергравитацию. Дуальности предполагают, что разные теории струн — это лишь разные выражения одной и той же фундаментальной концепции, которую называют М-теорией.

Нельзя говорить, что суперструны фундаментальнее супергравитации, и наоборот. Скорее, они являются разными представлениями одной и той же фундаментальной теории, и каждый подход удобен для работы со своим классом задач. Поскольку теории струн не содержат бесконечностей, они хорошо подходят для расчета того, что случается, когда несколько высокоэнергетических частиц сталкиваются и рассеиваются друг на друге. Однако они не слишком полезны для описания того, как энергия очень большого числа частиц искривляет Вселенную или образует связанное состояние, подобное черной дыре. В таких ситуациях требуется супергравитация, которая в основе представляет собой эйнштейновскую теорию искривленного пространства с некоторыми дополнительными типами материи. Именно эту картину я буду в основном использовать в дальнейшем.

Чтобы описать, как квантовая теория придает форму времени и пространству, будет полезно ввести концепцию мнимого времени. Термин «мнимое время» звучит так, будто заимствован из научной фантастики, но это вполне определенная математическая концепция: время, измеряемое так называемыми мнимыми числами. Можно представлять себе обычные действительные числа, такие как 1, 2, -3,5 и т. п., как соответствующие точки на оси, прочерченной слева направо: ноль в середине, положительные действительные числа — справа, отрицательные — слева (рис. 2.17).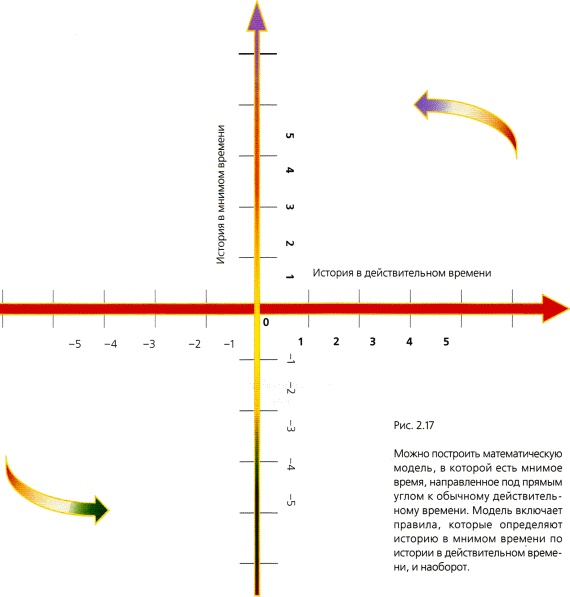

Мнимые числа правомерно изобразить соответствующими отсчетами на вертикальной оси: ноль опять посередине, положительные мнимые числа — вверху, отрицательные мнимые — внизу. То есть мнимые числа допустимо представлять себе как новый тип чисел, расположеных под прямым углом к вещественным числам. Поскольку это чисто математическая конструкция, они не нуждаются в физической реализации; никто, например, не может иметь мнимое число органов или мнимый счет по кредитной карте (рис. 2.18).