Большое космическое путешествие - читать онлайн книгу. Автор: Нил Деграсс Тайсон, Майкл Стросс, Дж. Ричард Готт cтр.№ 99

На рис. 21.4 струна изображена в центре, и заметно, где был сделан вырез, то есть где склеены два его края. Допустим, я нахожусь на Земле и рассматриваю квазар, расположенный за струной. Свет может долететь до меня по любой из двух этих прямолинейных траекторий (траектория 1 и траектория 2), проходящих по обе стороны от струны. Если склеить края пиццы на месте разреза так, чтобы лист бумаги сложился в конус, то две траектории световых лучей обогнут струну с разных сторон. Световые траектории искривятся под действием гравитационного линзирования. Именно такой эффект возникает, когда луч света пролетает мимо Солнца, мы обсуждали его в главе 19. Но траектории лучей света максимально прямолинейны. Я провел их по линейке. Если склеить «бумажную пиццу» наподобие конуса, то можно было бы провезти игрушечный грузовичок либо по траектории 1, либо по траектории 2 от квазара до Земли, никуда не сворачивая. Обе траектории являются геодезическими. Поскольку два луча света могут лететь по прямолинейным траекториям от квазара до Земли, мы видим две копии квазара по противоположные стороны от космической струны. Можно искать космические струны, высматривая в небе пары квазаров, так, чтобы два квазара располагались один напротив другого, словно пуговицы на мундире. Мы пока не нашли квазаров, линзированных под действием космической струны, но продолжаем искать.

Одно из замечательных свойств этой картины заключается в том, что длина двух световых траекторий может отличаться. Так, на рис. 21.4 траектория 2 немного короче траектории 1. То есть если я полечу на ракете от квазара к Земле на скорости 99,9999999999 % от скорости света, то смогу обогнать луч света, летящий по траектории 1, так как ему придется преодолеть большее расстояние. Я срежу путь и приду первым!

Хотя мы еще не видели космических струн, нам уже доводилось наблюдать подобное гравитационное линзирование в случае с галактикой, расположенной между нами и квазаром. Мы видим одинаковые копии далекого квазара QSO 0957+561 по обе стороны от линзирующей его галактики. Из-за искривления пространства-времени под действием этой галактики свет изгибается точно таким же образом, как и в случае космической струны. В таком случае яркость далекого квазара варьируется. Группе астрономов под руководством Эда Тёрнера, в состав которой также входили Томислав Кундич, Уэс Колли и я, удалось измерить в обеих «копиях» квазара один и тот же выброс, который был зафиксирован в одной копии с запаздыванием на 417 дней по сравнению с другой. Это малая толика того периода, за который свет этого квазара долетает до нас, – 8,9 миллиарда лет! Но если вам интересно, можно ли путешествовать быстрее света, то в данном случае ответ утвердительный: можно! Один луч света приходит на 417 дней раньше другого. Оба луча летели в вакууме с одинаковой скоростью, просто один из них срезал путь.

Итак, изучение квазаров-«близнецов» – один из способов поиска космических струн. До сих пор все известные случаи такого рода объясняются галактическим линзированием, но мы и ожидаем, что квазары, линзированные космическими струнами, должны встречаться реже, так что здесь нет ничего удивительного. Поиски продолжаются.

Космические струны натянуты и обычно вибрируют со скоростями примерно вдвое меньше скорости света. Точно как два луча света изгибаются навстречу друг другу, проходя по разные стороны от космической струны, так и два космических корабля, находящихся в состоянии покоя, можно подтянуть друг к другу, когда между ними стремительно движется космическая струна. Когда струна проходит между ними, они, набирая скорость, несутся друг к другу. Теперь допустим, что один из этих кораблей – Земля, а другой – реликтовое излучение (РИ). Двигающаяся струна дает небольшое доплеровское смещение в спектре расположенного за ней РИ. Если струна движется между РИ и нами слева направо, то РИ кажется чуть теплее слева от струны, чем справа. Мы ищем подобные эффекты. Колеблющиеся замкнутые струны, похожие на вибрирующие резиновые жгуты, могут давать гравитационные волны, и в будущем мы их также планируем искать при помощи аппаратов типа LIGO. Следовательно, есть ряд перспективных способов поиска космических струн.

Как можно было бы воспользоваться таким эффектом «срезания пути», который обеспечивает космическая струна? В 1991 году я нашел точное решение уравнений поля Эйнштейна в рамках общей теории относительности для двух движущихся космических струн. В этом решении две параллельные космические струны движутся одна мимо другой, как мачты двух шхун, плывущих ночью встречными курсами. Вертикальная струна 1 движется слева направо, а вертикальная струна 2 движется справа налево. Как должна выглядеть геометрия пространства вокруг двух этих струн?

Неудивительно, что на этот раз в пицце не хватает двух ломтиков. Поперечное сечение, перпендикулярное двум космическим струнам, напоминает лист бумаги с двумя вырезами, и из него можно сложить бумажный кораблик (рис. 21.5). Когда бумага разложена на столе, мы видим, где недостает двух кусков. Один начинается на струне 1 и продолжается вверх по странице, а второй начинается на струне 2 и продолжается вниз по странице. (Две струны вытянуты по направлению к вам, перпендикулярно странице.) Теперь можно срезать путь двумя способами. Если стартовать с планеты A на этом рисунке, то можно попасть на планету B по прямолинейной траектории, пролегающей между космическими струнами, она обозначена «Путь 2». Но есть и более короткий путь, который позволит вам добраться на планету B быстрее, это путь вокруг космической струны 1. Аналогично, другой сокращенный путь – путь 3 – позволяет вернуться с планеты B на планету A быстрее, чем по пути 2. Если стартовать с планеты A и отправиться на планету B на скорости 99,9999999 % от скорости света, то можно обогнать тот луч света, что летит непосредственно к планете B по пути 2. Путь 1 короче пути 2, поскольку не хватает одного «ломтика пиццы». Таким образом, можно отчалить от планеты A уже после того, как с нее по пути 2 улетит луч света, и прибыть на планету B раньше этого луча. Отправление с планеты A и прибытие на планету B – это два события, которые пространственноподобно разделены по пути 2; между ними в пространстве насчитывается больше световых лет, чем во времени – календарных лет. Вы обгоняете луч света и поэтому фактически движетесь со сверхсветовой скоростью, поскольку срезаете путь. Таким образом, некоторый наблюдатель, стремительно летящий влево, – назовем его Космо – сочтет два этих события одновременными. Поскольку его скорость меньше скорости света, он шинкует пространство-время под наклоном, как будто режет французский хлеб, и считает, что вы стартуете с планеты A и прибываете на планету B одновременно.

Теперь предположим, что в верхней части решения у нас будет стремительное движение вправо, которое захватывает и космическую струну 1, и Космо заодно с ней. Теперь струна 1 не стационарна, а быстро движется, и поскольку движение относительно, Космо больше не летит влево, а неподвижно застыл в центре. Космо смотрит на свои часы и видит, как вы в 12:00 улетаете с планеты A и в 12:00 прибываете на планету B. Если такой трюк вышел у нас однажды – выйдет и повторно.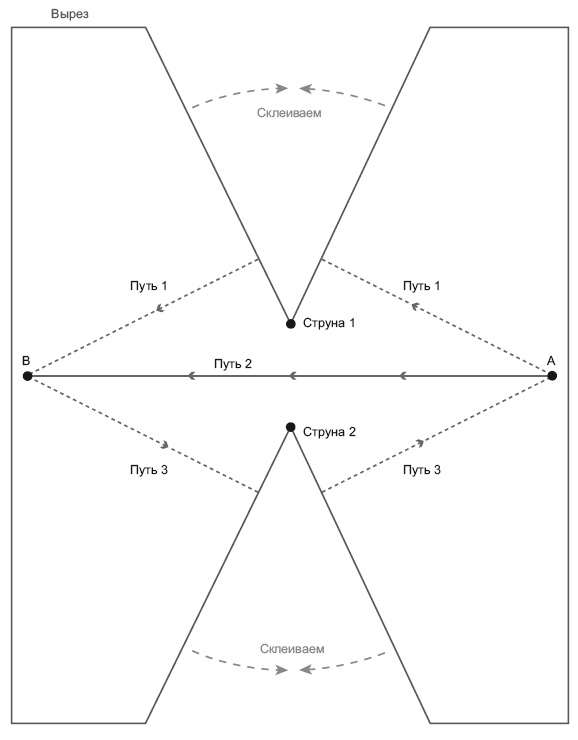

Рис. 21.5. Геометрия пространства вокруг двух космических струн. Иллюстрация адаптирована из J. Richard Gott, Time Travel in Einstein’s Universe, Houghton Mifflin, 2001