Большое космическое путешествие - читать онлайн книгу. Автор: Нил Деграсс Тайсон, Майкл Стросс, Дж. Ричард Готт cтр.№ 9

Она вышла в 1543 году и заставила людей задуматься. Поначалу Коперник опасался публиковать книгу и без огласки демонстрировал ее коллегам. Нельзя просто так взять и объявить, что Земля – больше не центр Вселенной. У могучей католической церкви было иное мнение на этот счет, духовенство продолжало утверждать, что Земля – центр.

Так говорил Аристотель. Древнегреческий философ Аристарх пришел к верному выводу, что Земля вращается вокруг Солнца, но аристотелевская точка зрения возобладала, и церковь упорно поддерживала ее, так как мнение Аристотеля согласовывалось с Писанием. Когда же Коперник опубликовал свою книгу? Он успел подержать ее в руках, лежа на смертном одре. Мертвых не репрессируют. Он возродил представление о Вселенной, выстроенной вокруг Солнца, так называемую гелиоцентрическую модель.

«Гелио» означает «Солнце». Ранее в науке были приняты геоцентрические модели. Их сформулировали Аристотель, Птолемей, а далее закрепили церковные эдикты.

Затем настал черед Кеплера. Кеплер поддерживал мнение Коперника, но с оговорками. Коперниковские орбиты имели форму идеальных окружностей. Но поскольку такая модель не соответствовала наблюдаемому движению планет, Коперник откорректировал ее, добавив небольшие круги-эпициклы (как и Птолемей в свое время). Все-таки модель не вполне точно описывала положения планет на небе. Кеплер понял, что модель Коперника нужно доработать. У него была информация – таблицы движения планет, составленные Тихо Браге, – и по этим таблицам он вывел три закона движения планет. Сегодня они именуются законами Кеплера.

Первый закон гласит: «Планеты движутся вокруг Солнца по эллиптическим, а не по круговым орбитам» (рис. 2.4). Что такое эллипс? С математической точки зрения у круга всего один центр, а у эллипса, можно сказать, два – они называются фокусами. Все точки окружности равноудалены от центра, а у всех точек на линии эллипса – одинаковая сумма расстояний до двух фокусов. Фактически круг – частный случай эллипса, где оба фокуса находятся в одной и той же точке. В продолговатом эллипсе фокусы значительно удалены друг от друга. Чем сильнее мы сблизим фокусы, тем ближе к идеальной окружности будет полученная фигура.

По Кеплеру, планетная орбита представляет собой эллипс, в одном из фокусов которого находится Солнце. Это утверждение уже было революционным. Древние греки считали, что поскольку Вселенная божественна, она должна быть совершенной, причем в греческой философии была конкретная концепция «совершенства». Круг – совершенная фигура; все точки окружности находятся на одинаковом расстоянии от центра; это и есть совершенство. Звезды движутся кругами, полагали древние греки. Эта философия сохранялась в течение тысячелетий.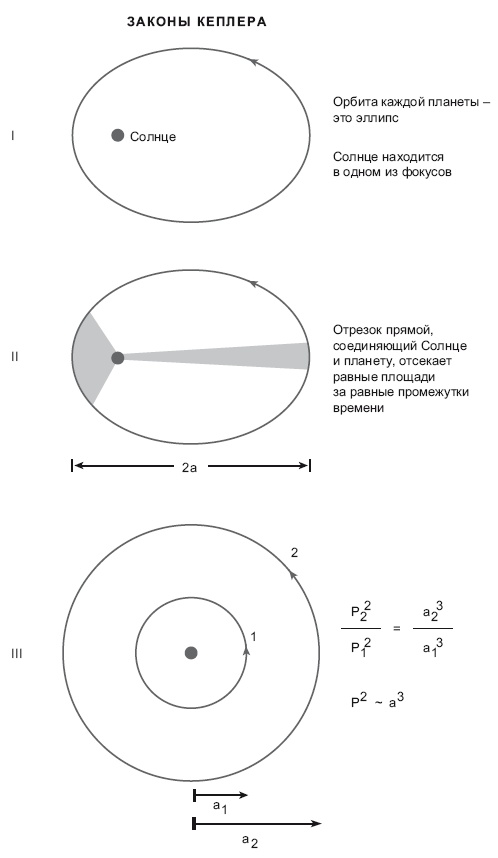

Рис. 2.4. Законы Кеплера. Величина a называется большой полуосью, она равна половине диаметра эллиптической орбиты. В случае круговой орбиты с нулевым эксцентриситетом большая полуось будет равна радиусу. Предоставлено Дж. Ричардом Готтом

А затем появляется Кеплер и говорит: «Люди, орбиты – это не окружности. Я взял таблицы Тихо и пришел к выводу, что орбиты – это эллипсы».

Далее он показал, что при вращении планеты скорость ее изменяется в зависимости от того, насколько она приближается к Солнцу. Представьте себе идеально круглую орбиту. Нет никаких причин на то, чтобы скорость движения планеты в разных точках окружности отличалась; планета всегда должна вращаться с одной и той же скоростью. Но с эллипсом все иначе. Когда скорость планеты будет максимальной? Тогда, когда планета будет ближе всего к Солнцу. Кеплер обнаружил, что планета движется наиболее быстро, будучи ближе всего к Солнцу, а чем дальше – тем медленнее она летит.

Кеплер обдумал эту задачу с геометрической точки зрения и решил: «Давайте измерим, как далеко планета успевает уйти, скажем, за месяц». Если планета расположена близко от Солнца и вращается быстро, то она будет заметать определенную площадь орбиты, так что получается вот такой неаккуратный широкий веер (см. рис. 2.4). Обозначим эту область A1. Проделаем такой же эксперимент в другой части орбиты, когда планета будет дальше от Солнца. Кеплер заметил, что чем дальше от Солнца планета, тем медленнее она движется и, соответственно, за то же время покрывает меньшее расстояние. Поскольку преодолеваемое расстояние меньше, планета пройдет за месяц область A2, напоминающую по форме длинный лепесток. Кеплеру хватило смекалки уловить, что область, заметаемая за месяц, всегда одинакова, независимо от того, каково расстояние от планеты до Солнца: A1 = A2. Так он сформулировал второй закон: «Отрезок прямой, соединяющий Солнце и планету, заметает равные площади за равные промежутки времени».

Из этого следует фундаментальный вывод, обусловленный сохранением углового момента. Если ранее вы этого термина не слышали, то, надеюсь, догадаетесь о его значении.

Угловым моментом пользуются фигуристы. Обратите внимание: когда фигурист начинает вращение, его руки вытянуты. А что потом? Спортсмен прижимает руки к телу, сокращая расстояние между руками и осью вращения, и, соответственно, ускоряется. Когда планета, движущаяся по эллиптической орбите, приближается к Солнцу, расстояние между ней и Солнцем уменьшается – соответственно, сама планета ускоряется.

Это явление именуется сохранением углового момента. Во времена Кеплера такого термина еще не существовало, но фактически он открыл именно угловой момент.

Третий закон Кеплера – гениален, просто гениален (вновь см. рис. 2.4). Он додумался до него не скоро. Первые два закона он дал практически экспромтом, считай за один вечер. На формулировку третьего ушло десять лет. Он пытался вывести взаимосвязь между расстоянием планеты от Солнца и тем, за какое время она проходит весь путь по околосолнечной орбите, ее период обращения. Внешним планетам требуется больше времени, чтобы сделать оборот вокруг Солнца, чем внутренним.

Сколько планет было тогда известно? Меркурий, Венера, Земля, Марс, Юпитер и самая популярная планета – Сатурн.

Многие третьекурсники говорили, что их любимая планета – Плутон. Поэтому они меня и недолюбливают. Как-то раз в «Роуз-центре Земли и Космоса» в Нью-Йорке мы собрались с коллегами и разжаловали Плутон из планеты в один из плутоидов – ледяных шаров, вращающихся на задворках Солнечной системы.

Греческое слово «планетос» означает «скиталец». Древние греки не считали Землю планетой, поскольку располагали ее в центре Вселенной. Причем древние греки выделяли еще две планеты, которые я не назвал, – какие? Это тела, также движущиеся на фоне звезд: Солнце и Луна. Таким образом, древние греки насчитывали семь планет. А названия семи дней недели в английском языке связаны с планетами или богами, которые с этими планетами ассоциировались. Так, Sunday (воскресенье) – день Солнца, Monday (понедельник) – день Луны. Суббота (Saturday) посвящалась Сатурну. Чтобы понять остальные названия, нужно обратиться к другим языкам. Так, пятница (Friday) названа в честь Фригг (Фрейи), норвежской богини любви, которая ассоциировалась с Венерой.