Большое космическое путешествие - читать онлайн книгу. Автор: Нил Деграсс Тайсон, Майкл Стросс, Дж. Ричард Готт cтр.№ 115

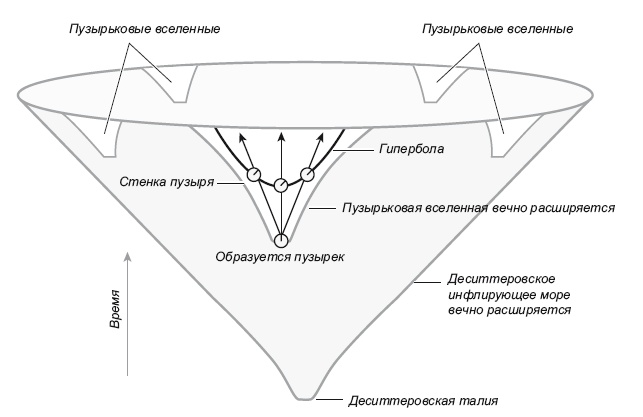
Рис. 23.3. Пузырьковые вселенные, образующиеся в инфлирующем море, – Мультивселенная. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

В разных пузырьковых вселенных могут действовать различные законы физики, если считать, что разные пузыри соответствуют туннелированию и скатыванию в разные долины космического ландшафта, причем значения различных физических полей от долины к долине могут отличаться. Законы физики, действующие в нашей Вселенной, могут оказаться лишь локальными «нормативными актами», что подчеркивают в своих работах Андрей Линде и Мартин Рис.

Важное свойство деситтеровской инфляционной модели таково: она должна начинаться с талии. Нам не нужен этап бесконечного сжатия, предшествующий талии. Борде и Виленкин продемонстрировали почему: на этапе сжатия также будут формироваться пузырьки и, следовательно, пузырьки будут расширяться в сжимающемся пространстве: сравнительно неплотные пузыри будут сливаться друг с другом и заполнять пространство. В результате получится инфлирующее море, которое так и не достигнет талии, а значит, не перейдет к этапу расширения. Возникнет просто сингулярность Большого схлопывания; пузырьки не будут обладать достаточной отрицательной энергией, чтобы на талии процесс пошел вспять. Итак, Борде и Виленкин пришли к выводу, что инфлирующая Мультивселенная начинается с конечного участка инфлирующего моря. Он может быть миниатюрным, всего 3 × 10^–27 см. Это не «ничто», но, пожалуй, «почти ничто» в любом мыслимом приближении.

Плотность энергии вакуума можно сравнить с отметкой высоты на ландшафте. Данная высота соответствует плотности энергии вакуума, то есть плотности энергии пустого пространства. Различные участки местности соответствуют различным значениям полей (например, поля Хиггса), порождающих энергию вакуума. Различные местоположения (разные значения полей) соответствуют разным высотам (разным значениям плотности вакуума). В настоящее время плотность вакуума очень низкая – мы почти на уровне моря. Но в юной Вселенной плотность вакуума должна была быть велика, как будто Вселенная была заперта в высокогорной долине (рис. 23.4).

Если шар окажется в такой долине, то он, в конечном итоге, будет неустойчив. Есть более низкоэнергетическое состояние, куда он может скатиться, – уровень моря. Но шар может остаться в долине, если со всех сторон его окружают высокие горы. В ньютоновской Вселенной такой шар ни при каких условиях не может скатиться вниз, но известен процесс, именуемый «квантовое туннелирование», позволяющий шару проскочить через гору и покатиться к морю ^[40].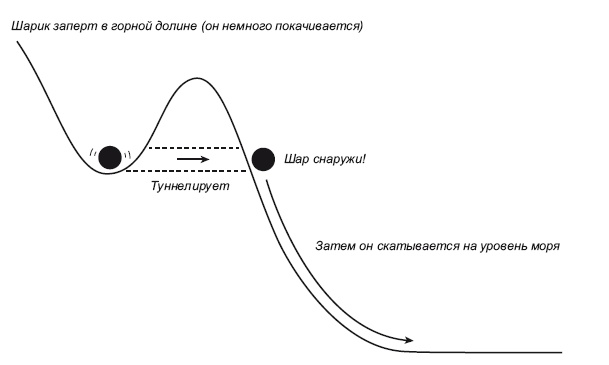

Рис. 23.4. Квантовое туннелирование. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Георгий Гамов открыл процесс квантового туннелирования. Таким образом он объяснил деление ядра урана. При распаде ядра урана выделяется альфа-частица (ядро гелия, в котором два протона и два нейтрона). Альфа-частицу удерживает в ядре сильное ядерное взаимодействие, приковывающее эту частицу к другим протонам и нейтронам. Сильное взаимодействие напоминает горный кряж, опоясывающий долину и заключающий альфа-частицу внутри ядра.

Но сильное ядерное взаимодействие является короткодействующим; если бы альфа-частице удалось каким-то образом вырваться из ядра, преодолев сильное взаимодействие, то она могла бы ускользнуть. Альфа-частица положительно заряжена и, следовательно, положительно заряженный массив ядра стал бы ее отталкивать. Частица покатилась бы по склону в сторону от ядра, набирая кинетическую энергию за счет электростатического отталкивания. По измеренной энергии, которой обладает альфа-частица, испускаемая при делении ядра урана, ученые научились вычислять, насколько высоко на склоне она находилась перед падением. Оказалось, что частица начинает путь внеядра урана! Как она туда попадает? Согласно квантовой механике, свет имеет корпускулярно-волновую природу, и такой же дуализм присущ другим объектам, которые мы называем «частицами», например альфа-частицам. В силу своей волновой природы альфа-частица не имеет четкой локализации, то есть подчиняется принципу неопределенности Гейзенберга. Гамов обнаружил небольшую вероятность того, что альфа-частица может «туннелировать» через ту гору, которая запирает ее в ядре, и внезапно оказаться далеко за пределами ядра, откуда она уже может покатиться вниз под действием электростатического отталкивания. Ситуация напоминает мне буддийский коан «Как утке выбраться из бутылки?» (горлышко которой слишком узкое). Ответ: «А утка уже снаружи!» Итак, квант альфа-частицы туннелирует через гору, и «альфа-частица уже снаружи». Вот второе достижение, за которое Гамов мог получить Нобелевскую премию.

В примере с пузырьковой вселенной на месте горной долины у нас будет первичная инфляционная вселенная (на талии деситтеровского пространства) с высокой плотностью вакуумной энергии. Вселенная была бы не прочь вечно расширяться, будучи в таком высокоэнергетическом состоянии, но спустя достаточное время возникнет шанс, что она туннелирует через гору и покатится по склону к морю, высвобождая энергию своего вакуума в виде кинетической энергии, из которой будут рождаться обычные элементарные частицы. Такое туннелирование – это мгновенное формирование пузырька, плотность энергии вакуума в котором чуть ниже, чем за пределами пузырька. Отрицательное давление вне пузырька сильнее отрицательного давления внутри пузырька, и из-за разницы давлений стенки пузырька расширяются. Расширение происходит все быстрее и быстрее, пока, наконец, этот процесс не разгоняется до субсветовой скорости. Тем временем внутри пузырька плотность энергии вакуума постепенно снижается (катится с холма к морю). Пока пузырек катится со склона, инфляция в нем продолжается. Когда он скатится на берег моря и вся его вакуумная энергия растратится по пути на образование элементарных частиц, инфляция остановится и начнется фридмановский этап. Именно такой сценарий независимо друг от друга описали в своих статьях Андрей Линде, а также Андреас Альбрехт и Пол Стейнхардт вскоре после выхода моей работы. Вне пузыря состояние вакуума остается «высокогорным», и инфлюирующее море продолжает стремительно, с ускорением расширяться. Я затрагивал вопросы, связанные с геометрией и специальной теорией относительности в контексте образования пузырьковых вселенных (сегодня этот феномен называется «Мультивселенная»), а тем временем Линде, Альбрехт и Стейнхардт подробно расписали физику частиц, обеспечивающую возникновение пузырьковых вселенных. Я настаивал, что для появления привычной для нас Вселенной инфляция в пузырьковой вселенной должна была продолжаться некоторое время. В моделях Линде, Альбрехта и Стейнхардта этот процесс разворачивался естественным образом: пузырьку требовалось некоторое время, чтобы постепенно скатиться со склона на уровень моря. Позже, в 1982 году, Стивен Хокинг опубликовал статью, в которой поддержал идею пузырьковой вселенной и показал, что под действием инфляции квантовые флуктуации увеличатся настолько, что станут проявляться в космологических масштабах и приобретут ровно такую форму, которая требуется для зарождения во Вселенной галактик и их скоплений ^[41]. Впоследствии такую структуру удалось проследить как в РИ, так и в распределении галактик (о чем мы рассказывали в главе 15), и эти данные блестяще согласовались с прогнозом инфляционной теории.