Красота в квадрате. Как цифры отражают жизнь и жизнь отражает цифры - читать онлайн книгу. Автор: Алекс Беллос cтр.№ 78

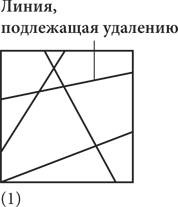
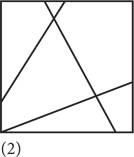
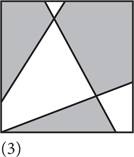
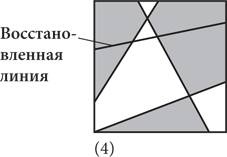
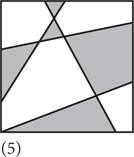
1) — рисунок, состоящий из одного ряда, может быть двухцветным;

2) — если рисунок, состоящий из n рядов, может быть двухцветным, то и рисунок с количеством n + 1 рядов тоже будет двухцветным.

Доказать истинность первого утверждения очень просто: достаточно провести через всю страницу прямую линию и заштриховать область с одной стороны. А вот для того, чтобы доказать истинность второго утверждения, понадобится немного поразмышлять.

Начнем доказательство с рассмотрения n + 1 линий, как показано на схеме 1 ниже. (Очевидно, что для иллюстрации данного примера для числа n нужно выбрать какое-то значение, поэтому мы должны проследить за тем, чтобы наше доказательство было применимо к любому числу n.)

Если удалить одну линию, у нас получится рисунок с количеством линий n, показанный на схеме 2. Предположим, рисунок с количеством линий n можно сделать двухцветным, как на схеме 3. Теперь давайте восстановим линию, убранную на первом шаге (схема 4), и с одной ее стороны поменяем цвет на противоположный, другими словами — белые фрагменты сделаем заштрихованными, а заштрихованные — белыми. В результате каждый сектор над линией расположен рядом с сектором под линией, имеющим другой цвет. Следовательно, у нас пролучился двухцветный рисунок с количеством линий n + 1 (схема 5).

Доказательство теоремы о двухцветном рисунке методом индукции

Иными словами, мы продемонстрировали, что второе утверждение истинно. Процесс доказательства методом индукции завершен: все рисунки могут быть двухцветными. (Это доказательство распространяется только на рисунки, образованные посредством вычерчивания линий на квадратном листе. То же самое касается и любого фигурного рисунка с «завитушками», когда перо начинает и прекращает двигаться в одной и той же точке, но по мере перемещения может рисовать петли, спирали и пересечения любой сложности. Однако это утверждение требует более сложного доказательства.)

Труд Евклида «Начала» стал самым важным текстом в истории математики, и не только потому, что он раскрыл информацию о простых числах, треугольниках и т. д., но и благодаря тому, как именно это было сделано. Красота этого текста состоит в его строгости. Евклид весьма скрупулезен. Он ничего не упрощает, не дает никаких оценок и не делает заявлений, которые не может доказать. Если вы согласитесь с тем, что десять исходных предположений Евклида верны, то вы должны принять и истинность всех 465 теорем, сформулированных в книге. «Начала» — это образец применения аксиоматического метода, свидетельство силы дедуктивного мышления.

Говорят, что «Начала» Евклида переиздавались на протяжении большего периода и в большем количестве экземпляров, чем любая другая книга, за исключением Библии. Это очень уместное сравнение, поскольку более двух тысячелетий труд Евклида считался священным текстом, а аксиоматический метод принимался в качестве догмы. Однако в XVII веке появились первые признаки «нечестивости». Евклид полагался на аксиомы и определения, которые по самой своей сути не требовали доказательств и, разумеется, не содержали внутренних противоречий. Но, как мы видели в предыдущей главе, бесконечно малой величине, или величине, которая представляет собой одновременно и нечто, и ничто, свойственна именно такая внутренняя противоречивость. Ньютон и его современники использовали концепцию бесконечно малых величин, поскольку она позволила им доказать множество новых теорем, хотя им и приходилось закрывать глаза на противоречие с догматами Евклида, которые это за собой влекло.

Однако со временем математики поняли: для того чтобы исчисление было свободно от внутренних противоречий, оно должно опираться на более прочный фундамент. Было решено положить в основу исчисления не бесконечно малые величины, а нечто более надежное — концепцию предела. После упрощения исходных предположений и уточнения определений родился новый раздел математики — математический анализ. Сейчас этим термином обозначаются все области, связанные с исчислением, непрерывностью и бесконечными процессами. Одним из первых знаковых достижений математического анализа стала теорема о промежуточном значении, о которой шла речь в начале главы, гласящая, что непрерывная кривая покрывает все точки, расположенные между ее минимумом и максимумом.

Присущая XIX столетию склонность к научной строгости нашла свое отражение не только в математическом анализе, но и в других областях, в частности в евклидовой геометрии. Внимательно проанализировав «Начала», немецкий математик Мориц Паш сделал невероятное открытие: в рассуждениях Евклида есть прорехи, которые до сих пор никто не заметил, несмотря на то что «Начала» — наиболее изученный учебник по математике за всю историю. Евклид считал само собой разумеющимся, что, если три разные точки лежат на одной прямой, значит, одна из них находится между двумя другими. Однако если бы Евклид придерживался собственных стандартов, ему следовало бы сформулировать это утверждение в виде аксиомы. Евклид совершил неосмотрительную ошибку, позволив своим глазам воздействовать на дедуктивный процесс. В 1899 году Давид Гильберт предложил новую, усовершенствованную евклидову систему, содержащую 21 постулат.

Числа тоже были тщательно проанализированы по-новому. Числа — это ядро всей математики, по сути — всей науки. Но что такое число и почему 1 + 1 = 2?

В 1879 году немецкий математик Готлоб Фреге опубликовал свой труд Begriffsschrift («Исчисление понятий»), в котором представил тщательно проработанную, имеющую собственные обозначения систему исчисления, позволяющую определить истинность и ложность утверждений. Это было рождение математической логики — использования математических рассуждений для анализа других математических рассуждений.

Фреге хотел дать четкий ответ на вопрос «Что такое число?». Для решения этой задачи он позаимствовал у своего современника Георга Кантора концепцию множества. В математике часто бывает так, что на первый взгляд простое слово означает нечто сложное. Но только не в случае с множеством. Множество — это всего лишь совокупность объектов, обладающих одним и тем же свойством. Множеством может быть ящик яблок, пелотон (лидирующая группа) велосипедистов или звездная галактика.