Красота в квадрате. Как цифры отражают жизнь и жизнь отражает цифры - читать онлайн книгу. Автор: Алекс Беллос cтр.№ 37

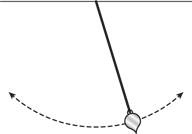
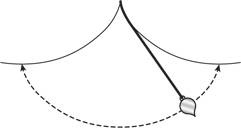
Однажды вечером в Париже в 1658 году Блез Паскаль лежал без сна в своей постели, терзаемый жестокой зубной болью. Будучи в прошлом знаменитым математиком, к тому времени он отказался от занятий этой наукой, чтобы сосредоточиться на теологии и философии. Пытаясь отвлечься от зубной боли, Паскаль решил поразмышлять о циклоиде. Боль прошла как по волшебству. Разумеется, он подумал, что это сам Бог призывает его продолжить изучение этой божественной кривой. Паскаль усердно работал над ней целых восемь дней, доказав за данный период много новых теорем. Однако, вместо того чтобы опубликовать, он сделал их темой международного состязания. Паскаль призвал своих коллег найти доказательство некоторых из полученных им результатов, пообещав сорок испанских золотых монет в качестве награды за первое место и двадцать — за второе. Вызов Паскаля приняли только два математика — Джон Уоллис в Англии и Антуан де Лалубер во Франции. Однако в представленных ими доказательствах были ошибки, поэтому Паскаль не присудил премию никому и опубликовал собственные результаты в виде небольшой книги, что привело обоих ученых в ярость. Кроме того, Паскаль получил письмо от Кристофера Рена, в котором шла речь об одном неизвестном Паскалю факте. Рен нашел ответ на, пожалуй, самый главный вопрос, касающийся циклоиды: какова ее длина? Рен доказал, что длина циклоиды ровно в восемь раз больше радиуса образующей окружности. Разумеется, когда Роберваль узнал об этом, он был возмущен и настаивал на том, что именно он это доказал много лет назад.

Интерес к циклоиде возрос еще больше, когда Христиан Гюйгенс открыл одно ее удивительное механическое свойство. В рамках работы над созданием часов нового типа голландский ученый экспериментировал с маятниками. Обычный маятник — это кусок нити с шаром у одного конца, как показано на рисунке ниже. Траектория движения шара представляет собой фрагмент окружности, причем чем дальше маятник отклоняется от вертикального положения, тем больше времени занимает одно полное колебание. Однако, для того чтобы использовать маятник для отсчета времени, Гюйгенсу было нужно, чтобы шар совершал колебания за одинаковые промежутки времени, независимо от амплитуды. Размышляя над задачей, поставленной его другом Паскалем, Гюйгенс понял, что для этого траектория движения шара должна представлять собой не что иное, как перевернутую циклоиду (см. второй рисунок), и что этого можно добиться, разместив две «щеки» в форме циклоиды у вершины маятника ^[96]. Когда маятник совершает колебание, его нить огибает каждую из «щек», меняя первоначальную круговую траекторию движения шара на траекторию в форме циклоиды. Как бы далеко от центра ни отклонялся шар циклоидального маятника, время его возвращения в начальную точку останется неизменным.

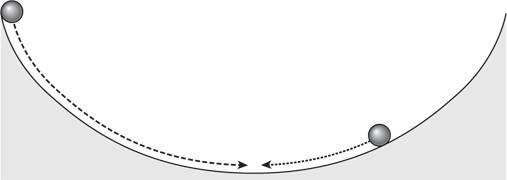
Обычный маятник и маятник, совершающий колебания между двумя циклоидами

Поражает еще один аспект данного свойства циклоиды. Представьте себе два шара, движущихся по совершенно гладкой, не создающей трения кривой в форме перевернутой циклоиды, как показано на рисунке ниже. Для того чтобы достичь нижней точки циклоиды, обоим шарам требуется одинаковое время, независимо от исходных позиций. Шар, находящийся выше, начал двигаться по более крутому склону, чем шар, расположенный ниже на кривой, что придало первому шару большее ускорение, а значит, и более высокую скорость. Эти два шара столкнутся в самой нижней точке кривой. Когда циклоиду объявили «кривой равных времен» (таутохроной, от греч. tautochrone: tauto — «тот же» и chrone — «время»), ученые пришли от нее в неописуемый восторг.

Траектория спуска шаров за равное время

История с циклоидой достигла своего апогея в конце XVII столетия. В новом научном журнале Acta Eruditorum, выходившем в Лейпциге, была опубликована статья, провозглашавшая следующее:

Я, Иоганн Бернулли, обращаюсь к самым выдающимся математикам в мире. Ничто так не привлекает интерес умных людей, как подлинная сложная задача, вероятное решение которой может принести славу и остаться вечным памятником… Если кто-то предоставит мне решение предложенной задачи, я публично объявлю его достойным всяческих похвал.

Задача, о которой говорил Бернулли и на которую он уже знал ответ, сводилась к поиску траектории наискорейшего спуска. Другими словами, какой формы должна быть горка, не создающая трения, для того чтобы объект прошел путь от одной точки к другой за кратчайшее время? Искомую кривую обозначили термином «брахистохрона» (греч. brachistochrone, от brachistos — «кратчайший» и chronos — «время»). Бернулли утверждал, что эта траектория не является прямой линией и представляет собой хорошо известную кривую. Если вы еще не догадались, вот вам ответ: эта кривая — циклоида. На представленном ниже рисунке показана траектория наискорейшего спуска из точки А в точки В и С. Поскольку циклоида имеет лишь одну форму, масштаб этой кривой необходимо изменить в зависимости от относительного положения начальной и конечной точек. Кривая либо только опускается (как в случае перемещения из точки А в точку В), либо сначала опускается, а затем поднимается (как при перемещении из точки А в точку С). Когда траектория опускается и поднимается, преимущества более крутого и длинного спуска компенсируют эффект замедления на повышающемся участке кривой в конце пути. Если сделать модель перевернутой циклоиды и пустить по ней шар, скажем из точки А в точку В, одновременно запустив шар и по прямой линии (обозначенной на рисунке пунктиром), ведущей из точки А в точку В, эффект будет просто поразительным, даже если вы заранее знаете, какой шар станет победителем в этой гонке. По сравнению с шаром, стремительно спускающимся по циклоиде, шар на наклонной прямой как будто катится по грязной дороге. Начиная с XVIII века для демонстрации брахистохроны в университетах и музеях начали сооружать деревянные циклоиды. С их помощью можно было демонстрировать и таутохрону. Для этого достаточно было разместить по одному шару с каждой стороны перевернутой циклоиды, и, независимо от того, с какой точки начнется движение этих шаров, они столкнутся друг с другом в самой нижней точке кривой.