
|
||
|
|
||
|
|
Онлайн книга - Тонкая физика. Масса, эфир и объединение всемирных сил | Автор книги - Фрэнк Вильчек
Cтраница 16

Излучение имеет место, когда частица выходит из равновесия со своим облаком. Тогда переупорядочение, которое восстанавливает равновесие в цветных полях, вызывает излучение глюонов или пар «кварк — антикварк», подобно тому как переупорядочение в атмосферных электрических полях вызывает молнии, а переупорядочение в тектонических плитах — землетрясения и извержения вулканов. Как кварк (антикварк или глюон) выходит из равновесия со своим облаком? Одним из вариантов может быть его внезапное выскакивание из виртуального фотона, как это происходило в экспериментах на БЭПК, которые мы обсуждали. Для достижения равновесия вновь образованный кварк должен нарастить свое облако, начиная от центра, где этот процесс инициируется его небольшим цветным зарядом. Соответствующие изменения невелики и постепенны, поэтому они производят лишь небольшие потоки энергии и импульса, то есть мягкое излучение. По-другому кварк может выйти из равновесия со своим облаком, если он будет вытолкнут квантовыми флуктуациями глюонных полей. Жесткое выталкивание может породить жесткое излучение. Однако поскольку присущий кварку цветной заряд мал, реакция кварка на квантовые флуктуации в глюонных полях часто бывает ограниченной, и поэтому жесткое излучение наблюдается редко. Вот почему более вероятно возникновение двух, а не трех струй. Связь наших фотографий с основами квантовой механики является еще более очевидной и не требует такого сложного объяснения. Мы в очередной раз обнаруживаем, что многократное повторение одного и того же действия каждый раз дает разные результаты. Мы видели это и раньше при работе с ультрастробоскопическим наномикроскопом, который делает снимки протонов; мы видим это, работая с машиной творческого разрушения, которая делает снимки пустого пространства. Если бы мир вел себя классически и предсказуемо, то, несмотря на вложенный миллиард евро, БЭПК представлял бы собой очень скучную машину: каждое столкновение просто воспроизводило бы результат первого, и у нас была бы лишь одна фотография для изучения. Вместо этого наши квантовые теории предсказывают, что одна и та же причина может порождать разные результаты. И мы находим этому подтверждения. Мы можем предсказать относительные вероятности для различных результатов. Основываясь на многократных повторениях, мы способны детально проверить эти предсказания. Таким образом, мы можем справиться с краткосрочной непредсказуемостью. А последняя, в конце концов, полностью совместима с долгосрочной предсказуемостью. Глава 7. Симметрия: отличия без различий
Основной идеей квантовой хромодинамики является симметрия. «Симметрия» — это общеупотребительное слово, и его смысл, как и смысл других подобных слов, является не вполне однозначным. Симметрия может означать баланс, приятные пропорции, регулярность. В математике и физике значение этого слова согласуется со всеми этими идеями, но является более четким. Мне нравится определение, согласно которому симметрия означает, что у вас есть отличие без различия. Юристы тоже используют фразу «отличие без различия». В этом контексте она обычно означает выражение того же самого, но другими словами. Вот пример от комика Алана Кинга: «Мой адвокат предупредил меня, что если я умру, не выразив свою последнюю волю, то я умру, не оставив завещания». Для понимания математической концепции симметрии рассмотрим пример. Мы можем построить симпатичную маленькую башню примеров, содержащую наиболее важные идеи в легко усваиваемой форме, в мире треугольников (рис. 7.1).
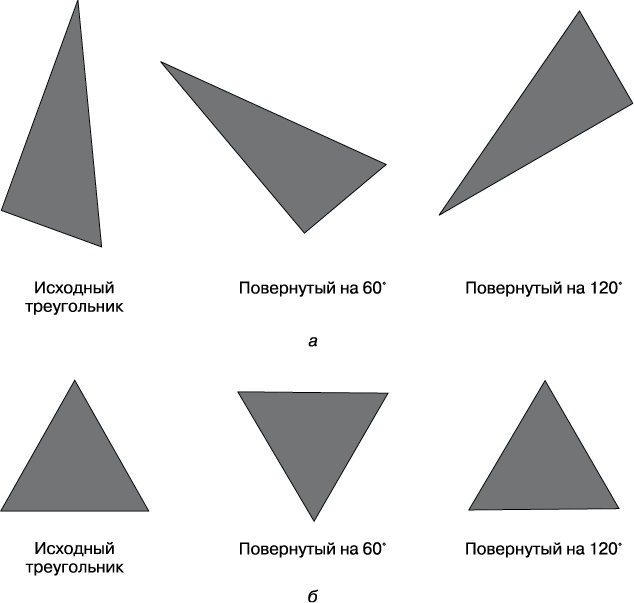
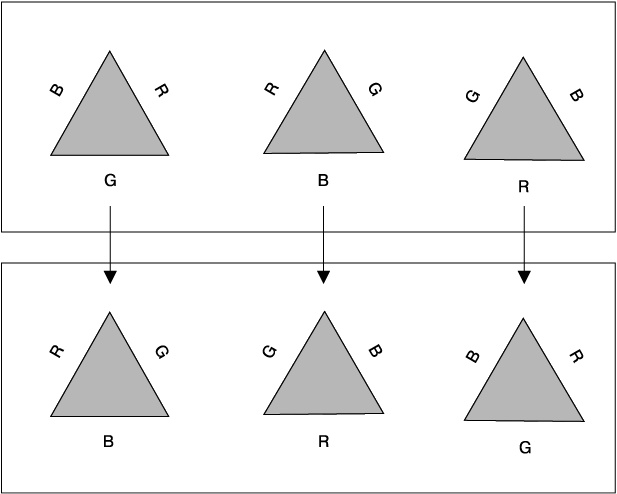
Рис. 7.1. Простой пример симметрии: а — вы не можете перевернуть неравносторонний треугольник, не изменив его; б — если вы повернете равносторонний треугольник на 120° вокруг его центра, он не изменится Вы не можете перевернуть большинство треугольников, не изменив их (см. рис. 7.1, а). Тем не менее равносторонние треугольники являются особенными. Вы можете повернуть равносторонний треугольник на 120 или 240° (то есть дважды), получив при этом ту же самую форму (см. рис. 7.1, б). Равносторонний треугольник обладает нетривиальной симметрией, поскольку она допускает отличия (между треугольником и его повернутыми версиями), которые, в конце концов, не создают каких-либо различий (повернутые варианты имеют ту же форму). И наоборот, если кто-то говорит вам, что треугольник выглядит так же, будучи повернутым на 120°, вы можете сделать вывод о том, что этот треугольник является равносторонним (или что человек лжет). Следующий уровень сложности проявляется тогда, когда мы рассматриваем набор треугольников с разными видами сторон (рис. 7.2). Конечно, если мы повернем один из них на 120°, мы не получим тот же треугольник — стороны не будут совпадать. На рис. 7.2 первый треугольник (RBG) поворачивается, превращаясь во второй треугольник (BGR), второй поворачивается, превращаясь в третий (GRB), а третий поворачивается, превращаясь в первый. Однако полный набор, содержащий все три треугольника, не изменяется [16].
Рис. 7.2. Более сложный пример симметрии. Равносторонние треугольники без различных «цветных» сторон (здесь цвета обозначаются так: R(ed) — красный, B(lue) — синий, G(reen) — зеленый) изменяются при поворотах на 120°; однако весь набор из трех треугольников возвращается в исходное состояние
С другой стороны, если кто-то говорит вам, что треугольник с тремя различными видами сторон наряду с некоторыми другими вещами выглядит по-прежнему после поворота на 120°, вы можете сделать вывод о том, что треугольник равносторонний, а также о том, что существует два равносторонних треугольника с различным расположением сторон (или о том, что человек лжет). Давайте добавим последний слой сложности. Вместо треугольников со сторонами разных цветов рассмотрим законы, связанные с этими треугольниками. Например, простой закон может заключаться в том, что при сжатии треугольника он аккуратно сворачивается так, что его стороны искривляются. Теперь предположим, что мы исследовали только треугольники RBG, так что мы действительно вывели закон сжатия только для этих треугольников. Если мы знаем, что вращение на 120° обеспечивает отличие без различий, то есть поворот на 120° определяет симметрию в математическом смысле, то мы можем сделать вывод не только о существовании других видов треугольников, но и том, что они тоже аккуратно сворачиваются при сжатии.
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно