Тайны чисел. Математическая одиссея - читать онлайн книгу. Автор: Маркус Дю Сотой cтр.№ 44

Простой арифметический прием подсчета букв означает, что любое сообщение, закодированное с помощью шифра подстановки, нельзя сделать секретным. Мария I, королева Шотландии, узнала это на собственном опыте. Она обменивалась посланиями, содержащими планы по убийству королевы Елизаветы I, с другим заговорщиком, Энтони Бабингтоном, при этом буквы в них заменялись странными символами (рис. 4.01).

Рис. 4.01. Шифр Бабингтона

На первый взгляд сообщения, посланные Марией, казались непроницаемыми, но при дворе Елизаветы был один из главных европейских знатоков по взламыванию шифров – Томас Фелиппес. Он не был привлекательным человеком, что ясно из следующего описания: «Малорослый, во всем худосочный, подслеповатый, с темно-золотистыми волосами на голове и светло-золотистой бородой, с оспинами на лице». Многие люди считали, что Фелиппес наверняка был в сговоре с дьяволом, раз обладал способностью понимать такие иероглифы, но он использовал тот же прием частотного анализа. Он взломал код, Мария была арестована и предана суду. Расшифрованные письма были тем свидетельством, которое в конечном счете привело королеву к смертной казни за участие в заговоре.

Когда стало понятно, что шифру подстановки присуща эта уязвимость, криптографы начали придумывать более изощренные способы кодирования, чтобы отразить атаки, использующие подсчет букв. Одна идея состояла в варьировании шифра подстановки. Вместо того чтобы использовать лишь один шифр подстановки для всего текста, вы можете поочередно использовать два различных шифра. Таким образом, если вы, к примеру, кодируете слово beef, то буквы е в нем будут закодированы по-разному, поскольку к первой из них применяется один шифр, а ко второй – другой. Может оказаться, что beef будет закодирована как PORK ^[14]. Чем более безопасным вы желаете сделать ваше сообщение, тем больше различных шифров нужно использовать в нем.

Конечно, в криптографии требуется приходить к компромиссу между надежностью шифра и легкостью его использования. В самом надежном виде шифра, называемом одноразовым блокнотом, используется свой шифр подстановки для каждой из букв сообщения. Его почти невозможно взломать, потому что нет совершенно никакого намека, как браться за шифротекст. Этот вид шифра также неудобен и громоздок, ведь приходится использовать свой шифр подстановки для каждой из букв сообщения.

Французский дипломат XVI в. Блез де Виженер считал, что для воспрепятствования частотному анализу будет достаточно переключаться между несколькими шифрами подстановки. Хотя шифр Виженера, как он стал известен, на самом деле является значительно более надежной формой кодирования, его все же можно взломать. Британский математик Чарльз Бэббидж в конечном счете нашел метод, позволяющий сделать это. Бэббидж по праву считается дедушкой компьютерного века: он был убежден, что машины можно использовать для автоматических вычислений, а в лондонском Музее науки можно увидеть реконструкцию его «Разностной машины» – механического аппарата для проведения вычислений. Именно систематический подход к решению задач способствовал тому, что в 1854 г. у него появилась идея, как взломать шифр Виженера.

Метод Бэббиджа задействует важное математическое умение – распознавание закономерностей. Первое, что вам необходимо выяснить, – между сколькими различными шифрами подстановки происходит переключение. Поскольку слово the, как правило, многократно встречается в любом открытом тексте, нужно попытаться заметить повторы одной и той же трехбуквенной последовательности, это может послужить ключом к определению количества шифров подстановки. Например, вы замечаете частые повторы последовательности AWR, причем количество разделяющих символов между различными употреблениями AWR кратно четырем. Это будет хорошим указанием на то, что используется четыре шифра.

Как только у вас есть эта информация, вы можете разбить шифротекст на четыре группы. В первую группу входит первая буква, пятая буква, девятая буква и т. д. Во вторую группу включены вторая буква, шестая буква, десятая буква и т. д. Для каждой из этих четырех групп использовался один шифр подстановки. Так что вы можете применить частотный анализ поочередно к четырем группам и взломать шифр.

После взлома шифра Виженера начался поиск нового способа надежно кодировать сообщения. Когда в 1920-х гг. в Германии была разработана шифровальная машина «Энигма», многие сочли, что было создано совершенное кодирование, которое невозможно взломать.

Принцип работы машины «Энигма» основан на переключении на другой шифр замены всякий раз после кодирования буквы. Так, если бы я захотел зашифровать последовательность аааааа (вероятно, она могла бы означать, что у меня приступ боли), то каждая буква а была бы закодирована по-своему. Элегантность машины «Энигма» заключалась в том, что смена одного шифра другим происходила автоматически и крайне эффективно. Сообщение печаталось на клавиатуре. Над ней находился другой набор букв, называемый «ламповой панелью», загоравшаяся буква отображала то, как кодировалась вводимая буква. Электрическое соединение клавиатуры с ламповой панелью происходило не напрямую, а через три вращающихся диска (ротора), в каждом из которых содержался клубок проводов.

Можно понять принцип работы машины «Энигма», если представить большой цилиндр, составленный из трех вращающихся барабанов. На верхнем основании цилиндра вблизи края расположены 26 отверстий, помеченных буквами алфавита. Чтобы закодировать букву, вы роняете шар в отверстие, соответствующее данной букве. Шар падает в первый барабан, у которого 26 отверстий вдоль обода наверху и 26 отверстий вдоль обода внизу. Верхние и нижние отверстия соединены трубками, которые не ведут напрямую от верхних отверстий к нижним, а извиваются сложным образом. В результате шар, попадающий наверху в барабан, выйдет внизу совершенно в другом положении. Средний и нижний барабан устроены схожим образом, но трубки, соединяющие их верхние и нижние отверстия, проложены по-своему. Когда шар падает из отверстия на дне третьего барабана, он попадает в конечную часть устройства, где 26 отверстий опять-таки помечены буквами алфавита.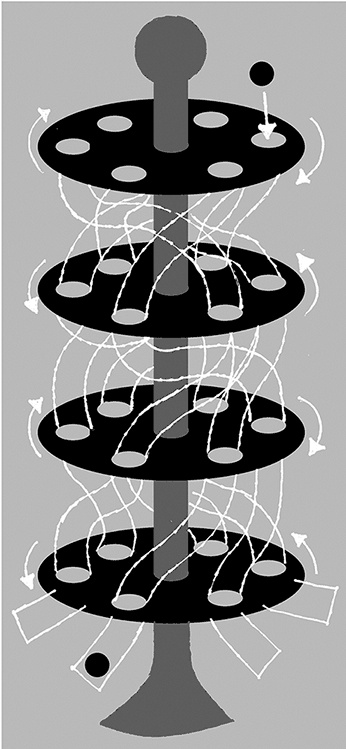

Рис. 4.02. Принцип работы шифровальной машины «Энигма»: опустите шар в отверстие наверху, соответствующее кодируемой букве. Барабаны вращаются после каждого кодирования, поэтому буквы всякий раз шифруются по-разному