
|
||
|
|
||
|
|
Онлайн книга - Тайны чисел. Математическая одиссея | Автор книги - Маркус Дю Сотой
Cтраница 28

Возможно, мы живем не на гипербублике, а на поверхности четырехмерного футбольного мяча. Некоторые астрономы полагают, что мы могли бы жить в форме, которая напоминает додекаэдр с 12 гранями, где как в мини-вселенной размером со спальню, когда вы достигаете одной из граней додекаэдра, то возвращаетесь в вашу вселенную через противоположную грань. Вероятно, мы совершили полный круг и вернулись к той модели, которую Платон предложил две тысячи лет назад. Согласно ей наша Вселенная заключена внутрь стеклянного додекаэдра, к поверхности которого прикреплены звезды. Возможно, современная математика наполнила смыслом эту модель, ведь противоположные грани этой формы теперь соединены и более не представляют стеклянных перегородок вселенной. Но какие другие формы могли бы быть у нашей Вселенной? Вспомните, как Пуанкаре провел классификацию всех возможных форм, которые могли бы быть у двумерных поверхностей, таких как поверхность нашей планеты. Поверхность может быть свернута как футбольный мяч, бублик, брецель с двумя дырками, с тремя дырками или с большим количеством дырок. Пуанкаре доказал, что какие бы другие формы вы ни постарались изготовить, их можно деформировать в сферу или брецель с дырками. А что же можно сказать о нашей трехмерной Вселенной – какая форма может быть у нее? Эта задача на миллион долларов называется гипотезой Пуанкаре. Она особенна, потому что в 2002 г. появились новости о ее решении российским математиком Григорием Перельманом. Его доказательство гипотезы Пуанкаре было проверено многими математиками, и теперь признано, что он действительно расклассифицировал все возможные формы, которые могла бы принимать наша Вселенная. Это была первая решенная задача на миллион долларов, но, когда в июне 2010 г. Перельману предложили получить премию, он, к общему изумлению, отказался от нее. Для Перельмана приз был не в деньгах, но в найденном решении одной из величайших задач в истории математики. До того Перельман уже отказался от медали Филдса, математического эквивалента Нобелевской премии. В наш век погони за славой и материальным достатком такой поступок человека, которого вдохновляет доказательство теорем, а не получение призов, представляется невероятно благородным. После того как математики признали доказательство Перельмана, можно утверждать, что они разобрались во всех возможных формах. Теперь дело за астрономами, наблюдающими за ночным небом: определить, какая из них лучше всего описывает неуловимую форму Вселенной. Решения
Воображая формы Разрез пересекает все шесть граней, и каждая грань добавляет ребро к образовавшейся новой грани. Эта форма должна быть симметрична, так что у вас получится шестиугольник. Расцепление колец Вот так можно расцепить два кольца, непрерывно деформируя их в тор с двумя дырками. 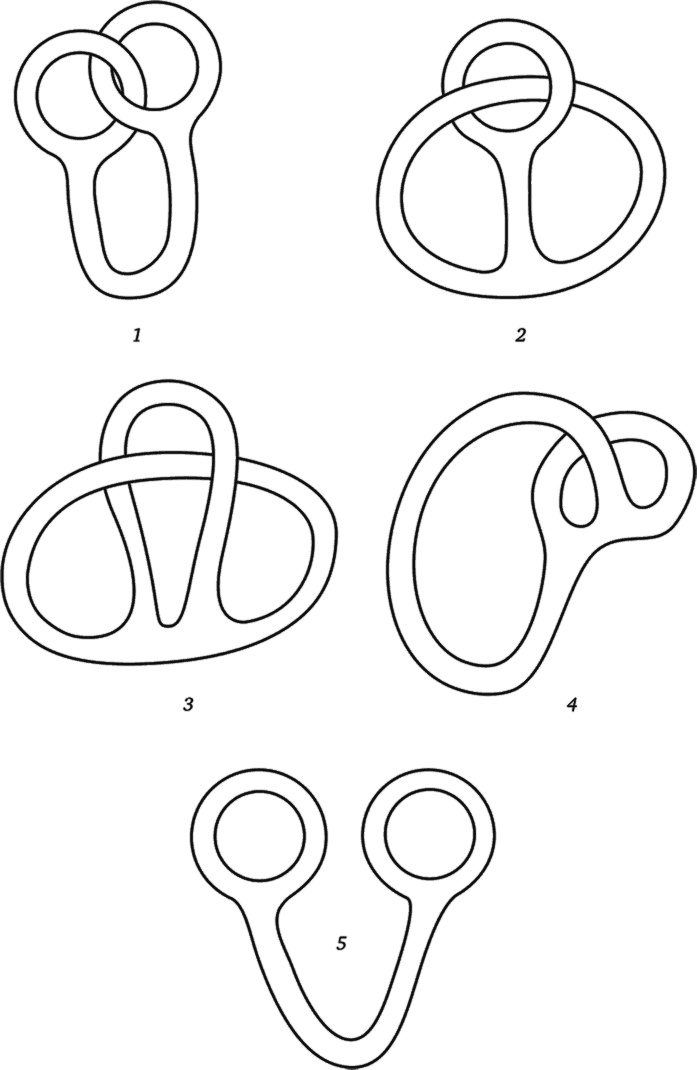
Рис. 2.45 Глава 3
Секрет победной серии Участие в играх является существенной частью человеческого опыта. Игры – это безопасный способ исследования ситуаций, происходящих в реальной жизни. «Монополия» – это микрокосм экономики, шахматы – поле сражения 8 × 8, покер – упражнение в оценке риска. Игры позволяют нам научиться предсказанию того, как при выполнении определенных правил будут развиваться события, и соответственному планированию своих действий. Благодаря им мы знакомимся со случайностями и непредсказуемостью, играющими столь большую роль в игре жизни, организуемой природой. От древних цивилизаций во всем мире нам досталось в наследство захватывающее разнообразие игр. Камешки, бросаемые в песок, палочки, подкидываемые в воздух, жетоны, вставляемые в прорези в деревянных колодках, соревнования с помощью рук и карт с изображениями на них… От древней игры манкала до «Монополии», от японской игры го до покерных столов Лас-Вегаса – в играх неизменно побеждает тот, кто лучше следует математическому, аналитическому подходу. В настоящей главе я покажу вам, как математика может быть секретным оружием к победной серии. Как стать чемпионом мира по игре «Камень, ножницы, бумага»?
«Дзян-кэн-пон» в Японии. «Ро-шам-бо» в Калифорнии. «Кай-бай-бо» в Корее. «Чин-чон-ча» в Южной Африке. В игру «Камень, ножницы, бумага» играют по всему миру. Правила очень просты. На счет «три» каждый игрок показывает рукой один из трех знаков: кулак, обозначающий камень, два разведенных пальца вместо ножниц или прямую ладонь, символизирующую бумагу. Камень побеждает ножницы, ножницы побеждают бумагу, и бумага побеждает камень. Если выпадают два одинаковых знака, то результат ничейный. Логическое обоснование первых двух побед достаточно очевидно: камень затупляет ножницы, ножницы режут бумагу. Но почему камень проигрывает бумаге? Лист бумаги – не слишком-то хорошая защита от камня, запущенного в вас. Но возможно, эта условность дошла до нас из Древнего Китая. В те дни прошение, подаваемое императору, символизировалось камнем. Император указывал на то, принял или нет он прошение, посредством листа бумаги, помещаемого под камнем или над ним. Если камень был покрыт листом бумаги, то в прошении отказывалось, а подавший его проигрывал дело. Происхождение этой игры довольно трудно проследить. Есть свидетельства, что в нее играли на Дальнем Востоке, она была распространена и у кельтских племен и, вероятно, даже у древних египтян, которые любили игры на пальцах. Но все эти цивилизации уступили первенство в изобретении этой игры разновидности ящериц, которая прибегала к ней в борьбе за выживание задолго до того, как Homo sapiens начал делать жесты. На западном побережье Америки обитает вид ящериц Uta stansburiana, более известный как обыкновенная пятнистая ящерица. У самца этого вида три возможных окраса – оранжевый, синий и желтый, и у каждого из них различная тактика спаривания. Оранжевые ящерицы – самые сильные. Они нападают на синих ящериц и побеждают их. Синие ящерицы больше желтых и охотно вступают с ними в битвы, нанося соперникам поражения. Но, хотя желтые самцы меньше синих и оранжевых, они выглядят как самки, что сбивает с толку оранжевых самцов. Поэтому оранжевые самцы, всегда готовые вступить в бой, не замечают, как желтые ящерицы проскальзывают у них под носом и спариваются с самками. Иногда желтых ящериц называют «пронырами» из-за используемого ими нечестного приема для обмана оранжевых ящериц. Итак, оранжевая побеждает синюю, синяя побеждает желтую, а желтая побеждает оранжевую – мы видим эволюционную версию игры «Камень, ножницы, бумага». 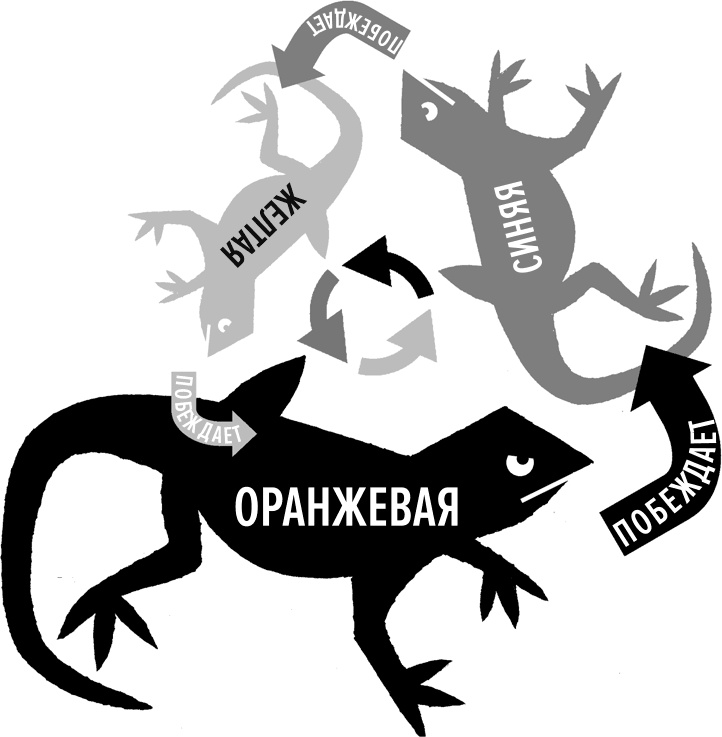
Рис. 3.01 Эти ящерицы участвуют в игре, передавая при этом свои гены. Было бы интересно узнать, разработали ли они какую-то стратегию выигрыша. Оказывается, в их популяции имеется шестилетний цикл, в начале которого доминируют оранжевые ящерицы, потом желтые, затем синие, а потом снова оранжевые. Появляющаяся последовательность в точности такая же, как у людей, которые пытаются победить в этой игре, сражаясь один на один. Если соперник слишком часто выкидывает «камень», вы начинаете показывать «бумагу», но оппонент, видя то, как участившаяся «бумага» побеждает его «камень», переключится на «ножницы», чтобы пресечь бумажную серию. Вы подмечаете это изменение в поведении и снова переходите на «камень».
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно