
|
||
|
|
||
|
|
Онлайн книга - Детский университет. Исследователи объясняют загадки мира. Книга первая | Автор книги - Улла Штойернагель , Ульрих Янссен
Cтраница 28

ПАСХА ПО ГАУССУ В 325 году н. э. Никейский собор постановил праздновать Пасху в первое воскресенье после первого полнолуния после дня весеннего равноденствия. В отличие от Рождества, Пасха выпадает каждый год на разные дни (как и Масленица). Но какой день правильный? Изобретательный математик Гаусс вывел формулу, с помощью которой можно рассчитать дату Пасхи на любой год. А посмотрите, как коротко и понятно будет выглядеть такое равенство, если записать его цифрами и математическими символами: 1 + 2 + 3 + … + 100 = (1 + 100) ×
Кажется, потихоньку становится понятно, почему математикам эта самая математика так нравится. С ее помощью можно сэкономить много времени. Можно удивить учителя. А как приятно бывает найти решение задачи! Занятно, но мы как раз сейчас решили одну задачу — ту, что была обозначена в заголовке этой главы: «Почему математики не умеют считать?» Ответ такой: настоящие математики вообще не считают, им лень это делать. С гораздо большим удовольствием они решают задачи. А арифметику оставляют калькуляторам. 
МЕЖДУНАРОДНАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА С 1959 года школьники со всего мира борются за победу в олимпиаде по математике. От каждой страны к участию в этих соревнованиях допускается шесть участников, которые за два дня должны решить шесть сложных задач. Победители, так же как и на настоящих Олимпийских играх, получают золотые, серебряные и бронзовые медали. Последняя большая математическая олимпиада состоялась в Гонконге в 2016 году. В ней приняли участие школьники более чем из восьмидесяти стран мира. Национальные отборочные турниры организуются в основном школами с математическим уклоном. Честно говоря, следует признать, что не все математики решают задачи так легко, как маленький Карл Фридрих Гаусс. Иногда приходится действительно много трудиться. Ведь задачи бывают запутанные и сложные. Главное при решении запутанных задач — сначала установить, в чем, собственно, задача состоит; так и говорят: «Определить задачу». Определение задачи — предпосылка для того, чтобы математики всего мира могли заняться поиском ее решения. У кого появляется идея, как подступиться к решению, формулирует теорему. Она описывает решение задачи, но этого недостаточно. Потому что теорему нужно доказать. Только при наличии доказательства всякий разумно мыслящий человек принимает выдвинутую теорему. Иначе говоря, математика похожа на игру. Только когда все игроки играют по одним всем известным правилам, игра приносит удовольствие. И действительно, математики ведут себя примерно как шахматисты. Хорошие шахматисты усердно читают книги по шахматам и анализируют партии других игроков. А чтобы победить других хороших шахматистов, они должны быть готовы к действительно трудным задачам. Они должны пробовать новые, необычные, фантастические ходы, до которых прежде никто не додумывался. Дети часто учатся такому лучше, чем взрослые. Поэтому в шахматах, так же как и в математике, встречаются настоящие вундеркинды, которые удивляют даже признанных мастеров. Например, таким вундеркиндом был тюбингенец Симон Брэндли. Уже в пятнадцать лет он посещал университетские семинары по математике и ставил в тупик своими вопросами изумленных преподавателей. В шестнадцать лет он окончил школу, а четырьмя годами позже стал кандидатом математических наук. 
Кстати, у шахматистов и математиков есть еще кое-что общее: они любят выигрывать и непременно хотят быть первыми в решении задач. Решать задачи весело, но это может быть и напряженной работой. Те, кто занимаются математикой в университете, должны быть готовы и к неудачам. Ведь математическая задача может быть либо решена, либо не решена. Тут, в отличие от других наук, не действует правило «отрицательный результат — тоже результат». В математике тот, кто не решил свою задачу, ничего не добился и не может написать даже завалящую статейку. Ему приходится думать дальше. Поэтому математиков часто можно узнать по потухшему взгляду. Даже в магазине, на концерте или на вечеринке с друзьями они продолжают размышлять над своей задачей. Даже по ночам они всё думают и думают. Иногда годы, а иногда и целые десятилетия. Один из известнейших математиков мира — англичанин Эндрю Уайлс. Он родился в Кембридже в 1953 году. Когда ему было десять лет, то есть в 1963 году, он однажды вечером зашел в библиотеку своего родного города. Ему захотелось просто покопаться в книжках. Случайно ему попалась книга о знаменитом математике Ферма. Эндрю начал ее читать и наткнулся на теорему Ферма. С тех самых пор она не выходила у него из головы. 
ТЕОРЕМА ФЕРМА Французский юрист и математик-любитель Пьер де Ферма однажды написал на полях старого учебника теорему, утверждающую, что уравнение аn + bn = cn не имеет решений в целых числах при степени больше двух, т. е. например, а4 + b4 = c4. Дальше он приписал, что нашел остроумное доказательство этому, которое, к сожалению, не вмещается на поля книги. С тех пор целые поколения математиков тщетно пытались найти это доказательство. Три века подряд умнейшие математики мира бились над доказательством теоремы Ферма, но безрезультатно. Маленький Эндрю решил заняться этой задачей. Он стал математиком и работал в лучших университетах мира — в Гарварде, в Принстоне, в Париже. И все это время он размышлял над теоремой Ферма. «Для меня это был личный вызов», — объясняет он. Только играя со своими детьми, Уайлс забывал о теореме Ферма, потому что их она совершенно не интересовала. Девятнадцатого сентября 1994 года произошло невероятное: «Совершенно неожиданно у меня случилось удивительное озарение». Этот день стал самым важным и волнующим моментом математической карьеры Уайлса. Он нашел решение — оно оказалось таким простым и элегантным, что минут двадцать Уайлс просто смотрел на свою запись, не веря глазам. Потом он пошел погулять, а вернувшись, проверил, на месте ли доказательство, и оно было там. Так, проразмышляв 31 год, Эндрю Уайлс доказал теорему, над которой математики бились триста лет.
|
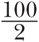 . А на случай, если учителю взбредет в голову заставить складывать числа не до 100, а до 200 или до 300, можно переделать это равенство так, чтобы оно подходило для всех подобных случаев. Для этого мы просто заменим число 100 на букву n: 1 + 2 + 3 + … + n = (1 + n) ×
. А на случай, если учителю взбредет в голову заставить складывать числа не до 100, а до 200 или до 300, можно переделать это равенство так, чтобы оно подходило для всех подобных случаев. Для этого мы просто заменим число 100 на букву n: 1 + 2 + 3 + … + n = (1 + n) ×
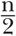 . Буква n в этом равенстве выступает в роли заместителя, ее можно заменить на любое натуральное число. Такая хитрость с заместителями чисел — гениальное изобретение, математики всего мира очень часто пользуются им. Конечно, в качестве заместителей не всегда используют именно n. Это могут быть и n, и x, и y, и a, и b — смотря по обстоятельствам. Но как бы они ни назывались, функция у них всегда одинаковая: замещать что-то другое. Они указывают на то, что уравнение справедливо не только для одного конкретного случая, а для всех подобных случаев.
. Буква n в этом равенстве выступает в роли заместителя, ее можно заменить на любое натуральное число. Такая хитрость с заместителями чисел — гениальное изобретение, математики всего мира очень часто пользуются им. Конечно, в качестве заместителей не всегда используют именно n. Это могут быть и n, и x, и y, и a, и b — смотря по обстоятельствам. Но как бы они ни назывались, функция у них всегда одинаковая: замещать что-то другое. Они указывают на то, что уравнение справедливо не только для одного конкретного случая, а для всех подобных случаев. Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно