Вычислительное мышление. Метод решения сложных задач - читать онлайн книгу. Автор: Пол Керзон, Питер Макоуэн cтр.№ 25

Пример игры 2. Нужно играть

Мы снова начинаем с того, что произвольно сдаем игрокам и дому небольшое количество карт. На этот раз у игрока 1 на столе шесть карт, у игрока 2 — четыре карты, и у дома тоже четыре карты.

Ситуация, когда ни в одной щели нет монет, а значит, М1 и М2 равны 0, легкая. Карты не перемещаются, для дома мы получаем 0 < 4, и на выходе 0: «Двух монет НЕТ». Условие (М1, М2) = (0, 0) корректно. Это показано на рис. 47.

Если монета есть только в щели 2, значит, (М1, М2) = (0, 1). Тогда карты игрока 2 идут вперед. Игрок 1 остается на месте, и на стол попадают четыре карты. На выходе мы имеем 0: «Двух монет НЕТ». Помните, что для получения 1 на выходе нам нужно, чтобы сумма карт на столе была больше (а не просто равна) Д. То есть ничего не меняется, и мы снова следуем правилу П1. Условие (М1, М2) = (0, 1) корректно.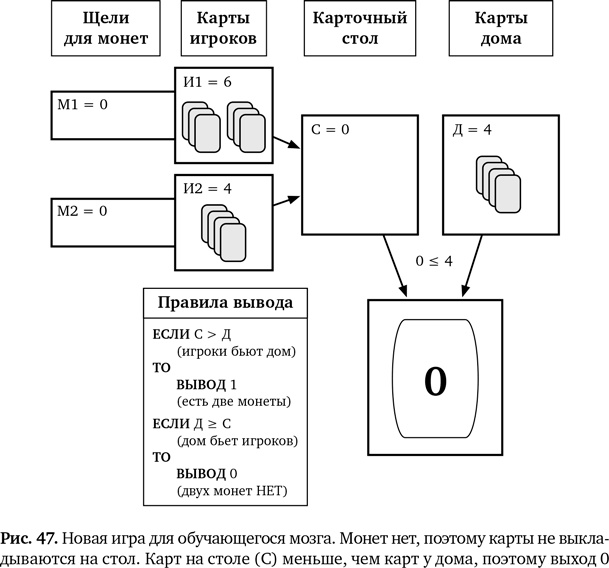

Теперь поместите одну монету в щель М1 и ни одной — в щель М2. И снова мы хотим получить на выходе 0, однако посмотрите на карты! На карточном столе у нас 6 ≥ 4, а значит, на выходе 1, и это неверно! Нужно применить правило П2. В нем говорится:

«ЕСЛИ сыгранная партия дает на выходе 1, но мы хотели получить 0, чтобы это соответствовало таблице выходов,

ТО заберите М1 карт у игрока 1 и М2 карт у игрока 2».

Это значит, что, поскольку М1 равно 1 и М2 равно 0, мы забираем карту у игрока 1, но не забираем у игрока 2. Новое значение И1 — 5 (6 − 1), а И2 остается равно 4.

Забрав карту из стопки игрока 1, мы возвращаем его карты. Мы не забрали ни одной карты игрока 2. Машина начала учиться.

Теперь мы выбираем другое условие и пробуем еще раз. Экспериментируя с этим примером, вы вернетесь к (М1, М2) = (1, 0), проходя через возможные вводные, и снова получите ошибку. И снова будет применено правило П2, и машина наберется еще немного опыта. На этот раз, когда карту убирают у И1, получается 4.

На этом этапе И1 = 4, И2 = 4, Д = 4. Итак, когда та же ситуация повторится снова, все получится, потому что в игре четыре карты игрока и четыре карты дома. Выход для (М1, М2) = (1, 0) будет 0: «Двух монет НЕТ», а это нам и нужно. Вы также обнаружите, что случай (М1, М2) = (1, 1) тоже дает верный результат. При этом условии конечное уменьшенное значение И1(4) + И2(4) = 8. У дома 4, а 8 > 4.

Наша машина научилась действовать правильно только благодаря игре и меняла карты, когда у нее не получалось. Правила игры — обучающий алгоритм.

Минус не помеха

Поэкспериментируйте с игрой сами. Вы обнаружите, что в какой-то момент придется применить все правила П1–П3 в зависимости от того, какие карты сданы в начале игры. Это поможет машине усвоить правильное поведение. Оно зависит от того, с чего вы начнете, и от порядка, в каком вы будете опускать монеты в щели (разные условия), но в конце концов даст результат. Если по правилам игры требуется взять карт больше, чем осталось у вас на руках, вы прибегаете к старой доброй «долговой расписке». Напишите записку c текстом «–1 карта» или «–2 карты» и продолжайте играть, проверяя, получите ли вы правильный ответ для каждого из условий. В конце останутся значения И1 и И2, которые будут соответствовать либо картам на руках, либо расписке, но игра все равно будет выучена.

Чем полезна игра с мозгом?

В этой игре вы создали самообучающийся модуль для мозга, чтобы вычислять логическую функцию «И». Он учится сообщать, есть ли монеты в щели 1 и в щели 2. Однако мы не программировали логическую функцию «И» — модуль сам научился ее вычислять. Использованный здесь принцип обучения основан на идее нейронной сети.

Нейронная сеть имитирует (моделирует) вычислительные операции мозга на базовом уровне — это абстракция. Миллиарды нервных клеток мозга, называемые нейронами,можно рассматривать как простые устройства обработки данных. Они связаны с другими нейронами с помощью особых отростков аксонов и получают сигналы из других частей нейронного контура. Если сигнал, поступивший в часть клетки, называемую синапс, достаточно силен (превышает весовой порог нейрона), то этот нейрон отправляет сигнал к другим, соединенным с ним.

Наша настольная игра моделирует один-единственный нейрон. В роли вводных сигналов используются монеты. Мы хотим, чтобы сигнал проходил (выход 1), только если присутствуют оба вводных сигнала (например, в обеих щелях есть по монете). Карты на руках представляют собой нейронный вес. Это меняющиеся элементы нейрона, которые помогают ему учиться. Количество карт, сданных дому, действует как весовой порог нейрона. Сначала нейроны не знают, как складывать поступающие сигналы. Они включаются случайно, подобно случайному числу карт, сданных в начале игры. Нейронные веса могут находиться где угодно. Но как один нейрон-кирпичик поймет, что делает мозг в целом? Ему необходимо учиться — и это делается по тому же принципу, что и в нашей карточной игре. Нейроны получают сигнал, который сообщает, был выход верным или неверным (поэтому весь процесс называют контролируемым обучением), и соответствующим образом меняют веса, укрепляя одни связи и ослабляя другие. При этом используются правила обучения, похожие на наши порождающие правила П1, П2 и П3. Веса, определяющие взаимосвязи, могут быть положительными (как карты на руках) или отрицательными (как «долговые расписки»).

Наша игра создает вычислительную модель работы нейронов. Мы сделали алгоритмическую версию нейронов, которая при симуляции действительно ведет себя нужным образом. Мы использовали игру с настоящими предметами, но то же самое можно сделать и с помощью программного обеспечения, которое создает модели с тысячами и даже миллионами нейронов. Такие модели позволяют исследовать, верно ли мы понимаем поведение нейронов. Будет ли наша модель вести себя как простой мозг?

Булевы операции

Итак, мы разобрались с биологическим обучением. Но что такое упомянутая логическая функция «И»? Это пример булевой операции. Булевы операции можно представить в виде таблиц (рис. 45) с булевыми значениями ИСТИНА (1) и ЛОЖЬ (0), на которых основана логика. Их в XIX в. разработал математик Джордж Буль. Математические способности этого удивительного человека позволили ему в 19 лет открыть собственную школу в Линкольне. Сделав блестящую карьеру, он неожиданно умер в возрасте 49 лет. Однажды Буль прошел больше двух миль под проливным дождем и стал читать лекцию прямо в мокрой одежде. Неудивительно, что у него начался сильный жар. К несчастью, жена математика Мэри, которая незадолго до этого уверовала в гомеопатию, решила лечить его средствами, «подобными причине болезни». Она стала поливать его водой из ведра прямо в постели. Стоит ли говорить, что состояние Буля ухудшилось, и 8 декабря 1864 г. он умер.

Работа Буля заложила основы для идеи логических вентилей, которые мы до сих пор используем в цифровых электронных схемах. В кремнии каждого микропроцессора сделаны миллионы логических вентилей, которые могут быстро вычислять сложные суммы. Точнее говоря, из кремния сделаны транзисторы, но конструктору трудно ориентироваться на них при создании новых разработок. Поэтому транзисторы группируют в логические вентили. Создавая логические вентили И (срабатывает, если на ввод подаются оба сигнала), ИЛИ (срабатывает, если есть хотя бы один сигнал) и так далее, конструктор думает о них и забывает о транзисторах — их можно игнорировать. Это обеспечивает первый уровень абстракции в создании цифровой электроники.