Сервисный компас - читать онлайн книгу. Автор: Антон Саввин cтр.№ 15

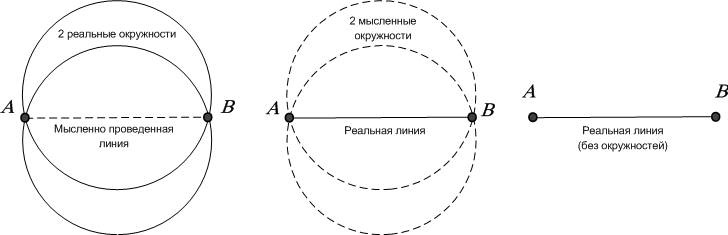
Рис. Две окружности, формирующие отрезок

или отрезок, не знающий о своем происхождении?

Ведь если посмотреть на окружающий мир, в нем нет ни одной прямой линии и тем более квадратов и кубов. Все вокруг состоит из соединения дуг окружностей или частей сфер разного радиуса. Все, что выполнено в виде прямых линий, идеальных поверхностей и точек излома, либо является абстракцией восприятия нашего сознания, либо создано искусственно руками человека.

Так что же мы тогда делаем на самом деле, решая задачу о квадратуре круга, сравнивая между собой квадрат и окружность? мы берем естественный квадрат и вписываем в него окружность или берем окружность и мысленно размещаем квадраты внутри и вовне?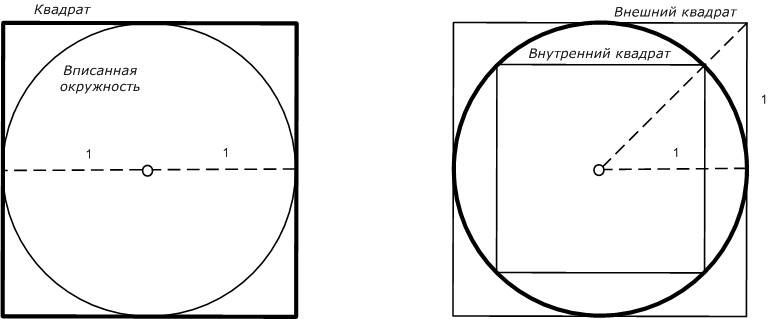

Рис. Окружность, вписанная в квадрат

или квадраты, размещенные вне и внутри окружности?

Похоже, что первична и естественна окружность единичного радиуса и двойного диаметра. Вокруг нее мы можем построить квадрат, в пропорциях которого и проявляется число Пи = 3,1415926…, или можем вписать квадрат, в пропорциях которого проявляется «Квадратный корень» и теорема Пифагора. Так что мы обнаруживаем не диаметр, творящий окружность, а окружность, проявляющая в себе диаметр, прямую линию и правильные многоугольники.

Все эти рассуждения в полной мере относятся не только к окружностям и квадратам, но и пространственным сферам и кубам. Именно пересечение окружностей в двумерном пространстве и сфер в трехмерном пространстве определяет все многообразие форм в природе, а уже соединяя мысленно или физически точки этих пересечений мы получаем фигуры, состоящие из вершин, углов, ребер и граней. В реальной природе нет прямых линий, а есть игра окружностей и гармония сфер.

Единственное, к чему можно условно применить понятие прямых – это противоположные направления: верх и низ, право и лево, север и юг… Но для этого за них надо зацепиться, как за точку опоры, которую так искал Архимед, объявить эту точку началом отсчета и построить ортогональные Декартовы оси координат. Но об этом позже, а пока, обратимся к Золотому сечению и второму волшебному числу «Фи» = 1.618..

Рискну немного переформулировать изречение великого древнего мыслителя, оперируя не натуральными, а иррациональными числами:

«Фи» порождает «Два». Два порождает все многообразие вещей.

Для проверки, мы вернемся к первой вибрации, разделяющей белое и черное. Здесь важно понимать, что белое и черное не отделяются друг от друга полностью, иначе они бы стали полностью независимы друг от друга. Чтобы быть во взаимной зависимости, они всегда находятся в смешанном состоянии, в какой-то строго определенной пропорции.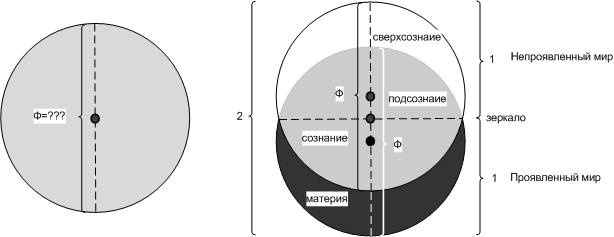

Рис. «Фи» порождает два

Иными словами, находясь в материальной нижней единичной половинке, я могу проявить только строго определенную часть нематериальной верхней половинки. Оставшаяся же верхняя часть всегда будет непроявленной внизу. И наоборот. Так что же это за пропорция? Зададимся двумя немного схожими вопросами:

Какое количество? Сколько? Какой объем? «серой массы» должно быть на старте, чтобы, разделяя ее на «белое» и «черное» получить в точности единицу «проявленного белого» плюс единицу «проявленного черного»?

В какой пропорции белое и черное надо смешивать между собой, чтобы запустить дальнейший самостоятельный процесс развития по единому правилу?

Проверим, что именно это количество и эта пропорция представляют собой Золотую пропорцию, или Золотое сечение, или число «Фи». Сделаем это сначала в одномерном пространстве на отрезке.

Поскольку я проверяю предположение, возьмем серый отрезок длиной «Фи»=1.618… и расщепим его на два отрезка – верхний и нижний, сделав параллельный сдвиг, так чтобы общая длина двух отрезков стала равной двум.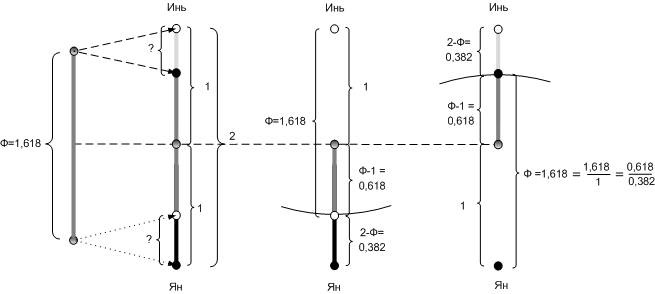

Рис. Золотое сечение отрезка длиной два.

Один отрезок становится верхним и белым, а второй – нижним и черным. Инь и Ян смешиваются в пропорции Золотого сечения. Такой же результат можно получить, взяв отрезок длиной два и отсекая циркулем сначала снизу, а потом сверху диаметр равный «Фи» = 1.618…

Более интересно это проявляется на плоскости. Окружность диаметра «Фи» растет до окружности диаметром два, одновременно порождая две подобные себе пересекающиеся окружности диаметра «Фи» – верхнюю и нижнюю, белую и черную.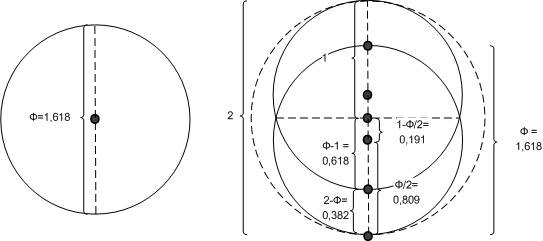

Рис. Золотое сечение окружности диаметром два.

Так вот в чем смысл Золотого Сечения?! Геометрическое Сечение, потому что черный низ частично проникает и влияет на белый верх, а белый верх частично проникает и влияет на черный низ. Эзотерически, это значит, что духовный мир отсекает и частично, проникает и влияет на мир материальный, и наоборот, материальный мир частично проникает и влияет на мир духовный. И все это происходит в строго определенной пропорции. Золотое Сечение, потому что единичный отрезок, например, в нижней проявленной части, чудесным образом оказался разделен в этой же пропорции и к нему может быть продолжен однотипный процесс попеременного сверху и снизу деления-сечения. При этом, получаемые более мелкие отрезки будут относиться друг к другу в одинаковом соотношении, повторяя первичную пропорцию. Взаимное проникновение белого и черного будет уходить в детали на микро уровень, постепенно превращая резкий дискретный переход от белого к черному в более плавный.

Чтобы понять красоту числа Фи, обратимся к музыке и математике. Будем ассоциировать направление вверх с увеличением частоты звука. Разделение отрезка в форме больший внизу, а меньший вверху дает мажорную триаду, или как говорят музыканты, мажорный аккорд, мажорное трезвучие. Разделение отрезка в форме меньший внизу, а больший вверху дает минорную триаду, или минорный аккорд.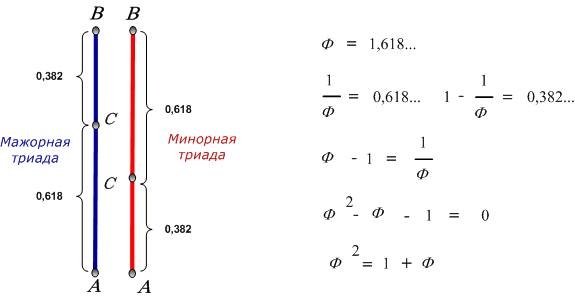

Рис. Мажорная и минорная триады. Свойства числа Фи.

До визуального ощущения красоты мира, остался всего один шаг. Около окружности можно не только вписывать или описывать квадраты. Можно построить прямоугольник, одновременно вписанный сверху и описанный снизу. И здесь нас ждет «Бинго»!!! Это оказался не прямоугольник, а Золотой квадрат со стороной равной «Фи»!!! Так вот откуда великий Леонардо брал пропорции в своих картинах?!