
|
||
|
|
||
|
|
Онлайн книга - Головоломки. Фокусы. Задачи. Игры. Развлечения | Автор книги - Яков Перельман
Cтраница 29

Легко видеть, что каждый играл не по одному разу, а по два: 
Итак, правильный ответ на головоломку таков: каждый из троих играл по два раза, хотя сыграно было всего три партии. Кто старше? (98)
Ни тот, ни другая не старше: они близнецы, каждому из них в данное время по 6 лет. Возраст находят простым расчетом: через 2 года мальчик будет на 4 года старше, чем 2 года назад, и притом вдвое старше; значит, 4 года – это возраст его 2 года назад, и, следовательно, сейчас ему 4 + 2 = 6 лет. Таков же и возраст девочки. Улитка (99)
Через 10 суток и 1 день. В первые 10 суток улитка поднимется на 10 метров, по 1 метру в сутки; в течение же одного следующего дня она всползет еще на 5 метров, т. е. достигнет верхушки дерева. (Обыкновенно неправильно отвечают: «Через 15 суток».) Пильщики дров (100)
Часто отвечают: в 1½ × 5, т. е. в 7½ минуты. При этом забывают, что последний разрез даст два метровых отрубка. Значит, распиливать 5-метровое бревно поперек придется не 5, а 4 раза; на это уйдет всего 1½ × 4 = 6 минут. В город (101)
Колхозник ничего не выгадал, а потерял. На вторую половину дороги он употребил столько времени, сколько отняло бы у него все путешествие в город пешком. Значит, он выгадать во времени не может, а должен потерять. Потерял он 1/15 того времени, какое нужно, чтобы пройти пешком половину дороги. В колхоз (102)
Решение этой задачи ясно из следующих выкладок: 24 км в гору и 8 км под гору – 4 часа 30 минут. 8 км в гору и 24 км под гору – 2 часа 50 минут. Умножив вторую строку на 3, имеем: 24 км в гору и 8 км под гору – 4 часа 30 минут. 24 км в гору и 72 км под гору – 8 часа 30 минут. Отсюда ясно, что 72 без 8, т. е. 64 километра под гору велосипедист проезжает в 8 часов 30 минут без 4 часов 30 минут, т. е. в 4 часа. Следовательно, в час он проезжал под гору 64: 4 = 16 километров. Сходным образом найдем, что в гору он проезжал в час 6 километров. Легко убедиться проверкой в правильности ответов. Автомобильное колесо (103)
Воздух внутри шины движется сразу в двух направлениях. От того места, где шина сжимается под грузом машины, воздух вытесняется и вперед – в еще несжатую часть шины, и назад – в сейчас освободившуюся от сдавливания часть. 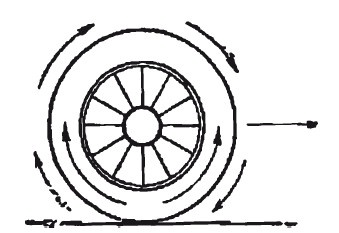
Эта старинная народная задача решается так. Спросим себя: на сколько во второй раз для заполнения мест на палках нужно было бы иметь больше галок, чем в первый? Легко сообразить: в первом случае для одной галки не хватило места, во втором же сидели все галки и еще двух не хватило; значит, чтобы занять все палки, нужно бы во второй раз иметь на 1 + 2, т. е. на 3 галки больше, чем в первый. Садится же на каждую палку на одну птицу больше. Ясно, что всех палок было три. Посадим на каждую палку по галке и прибавим еще одну – получим число птиц: 4. Итак, вот ответ на вопрос задачи: четыре галки, три палки. Два школьника (105)
Из того, что передача одного яблока уравнивает их число у обоих школьников, следует, что у одного на 2 яблока больше, чем у другого. Если от меньшего числа отнять одно яблоко и прибавить к большему числу, то разница увеличится еще на 2 и станет равна 4. Мы знаем, что тогда большее число будет равно двойному меньшему. Значит, меньшее число тогда будет 4, а большее – 8. До передачи одного яблока у одного школьника было 8–1 = 7, а у другого 4+1 = 5. Проверим, становятся ли числа равными, если от большего отнять одно яблоко и прибавить к меньшему: 7 – 1 = 6; 5 + 1 = 6. Итак, у одного школьника было 7 яблок, а у другого – 5. Цена пряжки (106)
Вы, вероятно, решили, что пряжка стоит 8 копеек. Если так, то вы ошиблись. Ведь тогда пояс был бы дороже пряжки не на 60 копеек, а всего на 52 копейки. Правильный ответ: цена пряжки 4 копейки. Тогда пояс стоит 68 – 4 = 64 копейки, т. е. на 60 копеек дороже пряжки. Сколько стаканов? (107)
Сравнивая первую и третью полки, мы замечаем, что они отличаются друг от друга следующим: на третьей полке один лишний сосуд среднего размера, зато нет трех малых сосудов. А так как общая вместимость сосудов каждой полки одинакова, то, очевидно, вместимость одного среднего сосуда равна вместимости трех малых. Итак, средний сосуд вмещает 3 стакана. Теперь остается определить вместимость большого сосуда. Заменив на первой полке средние сосуды соответствующим числом стаканов, мы получаем один большой сосуд и 12 стаканов. Сравнив это со второй полкой, соображаем, что один большой сосуд вмещает 6 стаканов. Бочки меду (108)
Задача решается довольно легко, если сообразить, что в 21 купленной бочке было меду 7 + 3½, т. е. 10½ бочки. Значит, каждый кооператив должен получить 3½ бочки меду и 7 бочек тары. Выполнить дележ можно двояко. По одному способу кооперативы получают: 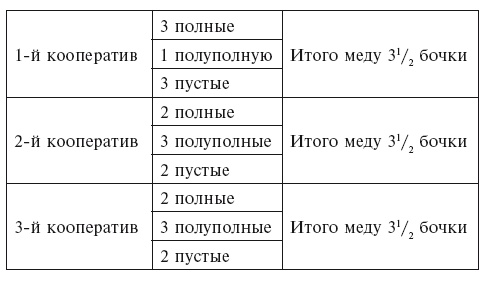
По другому способу кооперативы получают: 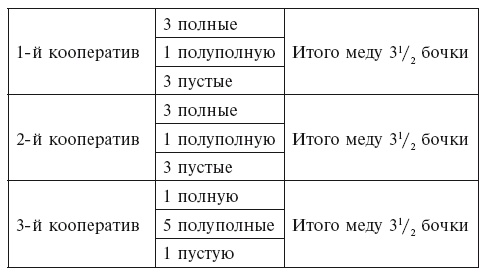
Продажа яиц (109)
Очевидно, крестьянка принесла на базар нечетное число яиц. Тогда половина всех яиц состояла из нецелого числа, а прибавка половины одного яйца превращала это число в целое. Что же это было за число? Начнем с конца. После того как вторая покупательница взяла половину оставшихся яиц и еще ½ яйца, у крестьянки оказалось только одно яйцо. Значит, одно яйцо и еще ½ яйца составляют вторую половину того, что осталось после первой покупательницы. Отсюда узнаем, что после первой покупательницы осталось 1½ + 1½, т. е. 3 яйца. Прибавив У яйца, получаем половину всего числа яиц, бывших у крестьянки. Итак, крестьянка принесла на базар 3½ + 3½, т. е. 7 яиц. (Проверьте этот ответ.)
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 Перейти к Примечанию
Перейти к Примечанию
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно