Камень ломает ножницы. Как перехитрить кого угодно: практическое руководство - читать онлайн книгу. Автор: Уильям Паундстоун cтр.№ 26

В настоящее время известно, что закон Бенфорда применим ко всем видам данных, которые не догадался проверить даже сам неутомимый автор. Известно также, что закон Бенфорда не применим ко многим числовым комбинациям (телефонные номера, обозначение возраста и веса, номера карточек социального страхования, коэффициенты умственного развития, победившие номера лотерейных розыгрышей и почтовые индексы). Примером может служить вес взрослых американцев. Совершенно очевидно, что 1 – самая распространенная первая цифра, ее доля гораздо выше, чем 30 процентов, предсказанных законом Бенфорда. Самая редкая – шестерка, даже реже, чем в распределении Бедфорда: немногие мужчины весят от 60 до 69 и от 600 до 699 фунтов.

Неприменим закон Бенфорда и к назначенным номерам, таким как номер телефона или карточки социального страхования. Тот, кто назначает номера, использует все или почти все возможные варианты. Номера, начинающиеся на 1, встречаются так же часто, как и те, которые начинаются с любой другой цифры.

Те, кто обладает математической интуицией, могут прийти к тому же выводу самостоятельно. Для всех остальных это неразрешимая загадка. Почему закон Бенфорда применим к номерам домов на улице, но не применим к почтовым кодам? Откуда в газете New York Times знают, будто числа, начинающиеся на 1, нужно упоминать в шесть раз чаще, чем те, которые начинаются на 9?

Закон Бенфорда справедлив для некоторых чисел, отражающих результаты измерений, например, городского населения или сумм, списанных с кредитных карт. Попробуем привести быстрое и интуитивное объяснение. Представьте, что вы положили на счет для инвестиционных операций 1000 долларов, которые удваиваются каждые десять лет. Первая цифра баланса вашего счета будет оставаться 1 на протяжении первых десяти лет. Сумма будет увеличиваться до 1100, 1200, 1300 долларов и так далее, до 1900, пока в конце первого десятилетия не достигнет 2000 долларов.

До следующего удвоения пройдет еще 10 лет. За это время сумма на счете постепенно увеличится с 2000 до 3000, а затем до 4000 долларов. Это значит, что на 2 и 3 в качестве первых цифр баланса счета приходится столько же времени, сколько на цифру 1.

В третьей декаде сумма на счете увеличится с $4000 до $8000, причем первыми цифрами будут 4, 5, 6 и 7. На протяжении четвертого десятилетия сумма увеличится до 16 000, и первыми цифрами сначала будут 8 и 9, а остальное время снова 1.

Итак, в сумме на инвестиционном счете 1 будет присутствовать больше времени, чем 2, 2 больше, чем 3, и так далее. Если выбрать случайный момент времени, то вероятность каждой из девяти цифр оказаться на первом месте будет точно соответствовать распределению Бенфорда.

В нашем мире есть множество вещей, от колоний микроорганизмов до социальных сетей, которые растут экспоненциально, хотя и не обязательно так занудно, как в моем примере. Но когда естественный рост рассеивает числа на несколько порядков величины, они приближаются к распределению Бенфорда. Если бы шимпанзе бросала дротик дартса в листок с финансовыми отчетами или ценами на бирже, то попадания с достаточной точностью соответствовали бы закону Бенфорда.

Закон Бенфорда напоминает, что числа – это искусственный способ отображения количественных соотношений в окружающем нас мире. Как писал сам Бенфорд, «в действительности это теория явлений и событий, а числа всего лишь играют незначительную роль безжизненных символов живого».

«Я подумал, что если предсказуемые закономерности для чисел действительно существуют, то аудиторы, наверное, смогут определить, какие данные соответствуют действительности, а какие вымышлены», – вспоминал Марк Нигрини.

Бухгалтеры и налоговые органы были бы рады иметь формулу для определения, какие цифры показаны честно, а какие нет. Нигрини быстро решил: его диссертация будет посвящена применению закона Бенфорда для выявления финансового мошенничества.

Он обнаружил, что после статьи Бенфорда на эту тему почти ничего не написано. Единственным, кто увидел практическую ценность открытия, оказался Хэл Вэриан (в настоящее время главный экономист Google). В 1972 г. Вэриан предложил использовать закон Бенфорда в качестве «индикатора чепухи». В политике решения основываются на сложных прогнозах издержек и выгод. Цифры в этих прогнозах должны соответствовать распределению Бенфорда, утверждал Вэриан. Если это не так, значит, составитель прогноза брал цифры с потолка или подгонял в соответствии со своими целями.

Вэриан не стал развивать эту идею – как и другие. Это подогрело энтузиазм Нигрини, но не его руководителя. «Он хотел бы, чтобы я был восьмидесятым ученым, исследовавшим этот вопрос», – объяснял Нигрини. Он настоял на теме диссертации, однако одобрение получил только после того, как написал две трети текста. Четыре месяца спустя работа была закончена.

Идея Вэриана и Нигрини может быть проиллюстрирована. Имея массив чисел, вы можете нарисовать столбиковую диаграмму (гистограмму), показывающую, сколько раз каждая цифра появляется первой. Просто сосчитайте, сколько чисел начинается с цифры 1, сколько с 2 или 3, и так далее. Для честных данных, подчиняющихся закону Бенфорда, диаграмма будет выглядеть так: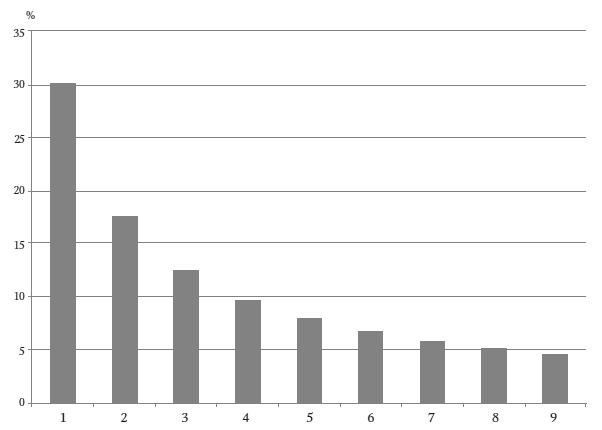

Закон Бенфорда

Гладкая кривая – это закон Бенфорда в визуальной форме.

Блестящая идея Вэриана и Нигрини состояла в том, что люди, фальсифицирующие цифры, не знают о законе Бенфорда. У растратчика или налогового мошенника нет причин думать, что какая-либо цифра должна встречаться чаще, чем другие. Поэтому массив искусственных чисел должен иметь равномерное распределение первых цифр.

Как бы то ни было, это упрощенная идея. Эксперименты по имитации случайности (о них не было широко известно) уже показали, что в сфабрикованных числах все цифры почти никогда не используются в равной мере. Альфонс Чапанис представил гистограммы полученных результатов, и распределение в них равномерным не было.

Другая проблема в том, что честные финансовые данные чаще всего в точности соответствуют кривой Бенфорда, но иногда – нет. И заранее бывает трудно сказать, с каким случаем вы имеете дело. Одним из таких примеров могут служить данные продаж магазина, где все товары стоят 99 центов. Анализ выявит большое количество девяток. Как замечает Нигрини, это указывает, что цены выдуманы, специально разработаны людьми как часть маркетинговой стратегии. Но если вы руководите таким магазином, это ваша реальность, а не мошенничество. Можно найти множество других ситуаций, когда природа бизнеса способствует распределению первых цифр, не отвечающему закону Бенфорда – по абсолютно невинным причинам.

Тем не менее, основная идея Нигрини оказалась верна: придуманные цифры отличаются от настоящих. Он стал частым гостем в здании суда Цинциннати, где разбирал преступления, в которых фигурировали цифры.

Один из первых исследованных им случаев мошенничества произошел в Аризоне. Уэйн Джеймс Нельсон, 43-летний менеджер отделения государственного казначейства в Аризоне, начал короткую карьеру растратчика с того, что выписал чек на 1927,48 доллара от штата Аризона на имя фиктивного поставщика. За следующие несколько дней он выписал еще 22 фальшивых чека на общую сумму почти 1,9 миллиона долларов.