Искусство думать. Латеральное мышление как способ решения сложных задач - читать онлайн книгу. Автор: Эдвард де Боно cтр.№ 8

На рис. 1 приведена простая, зрительно воспринимаемая ситуация, изображенная черным цветом на белом фоне. Она достаточно проста, чтобы мы могли воспринять ее как единое целое и, следовательно, рассматривать как единичное восприятие. Для восприятия приведенной ситуации требуется только зрение.

Простота этой ситуации и ее полная доступность визуальному восприятию облегчают наблюдение за процессом мышления, но не мешают ей служить отражением других, более сложных ситуаций, для восприятия которых наряду со зрением могут потребоваться и другие органы чувств.

Эта наглядная ситуация имеет форму геометрической фигуры, достаточно простой, но все же незнакомой – в том смысле, что она не имеет определенного названия. Для ее описания недостаточно одного слова, как это имеет место в случае квадрата, шестиугольника или креста.

Эта фигура настолько проста, что для ее изучения достаточно просто рассмотреть ее. В ней нет ничего, что требовало бы отдельных усилий для понимания или объяснения.

На протяжении всего этого упражнения задача понять фигуру будет для наглядности заменена задачей описать ее человеку, который ее не видит. Описание ситуации другому человеку сходно с ее описанием самому себе – а это, по сути, и есть процесс понимания любой ситуации.

Необходимость совершить действие является одним из наиболее сильных стимулов понять ситуацию. В наших примерах требуемое действие состоит в том, чтобы описать предлагаемые фигуры другому человеку.

Поскольку в языке нет общепринятого слова для описания этой фигуры, а знакомые слова – это единственный дозволенный способ коммуникации, следует попытаться описать незнакомую геометрическую фигуру с помощью знакомых слов.

Итак, эта фигура может быть описана только посредством уже известных терминов. Ее, например, можно сравнить с какой-нибудь знакомой фигурой и описать их различия. Однако более общий метод состоит в том, чтобы расчленить незнакомую фигуру на знакомые составные части, назвать их и указать принцип их соединения.

На рис. 2 показан один из способов деления фигуры, представленной на рис. 1. Вот как может выглядеть описание, основанное на таком делении:

1. Два параллельных бруска, разделенные двумя более короткими перекладинами, чуть отстоящими от концов брусков;

2. Горизонтальная балка, удерживаемая на другой такой же горизонтальной балке двумя вертикальными стойками;

3. Прямоугольник, у которого две короткие стороны слегка сдвинуты к центру.

Есть множество других способов описать приведенный здесь конкретный вариант разделения фигуры. Деление производится исключительно в уме, слушатель получает лишь описание составных частей фигуры и их соотношений, что позволяет ему мысленно составить всю фигуру. Это напоминает перевозку громоздкого механизма, который приходится разобрать на мелкие и более удобные для транспортировки части и в таком виде передать получателю, приложив инструкцию по сборке.

Представленный на рис. 2 принцип деления фигуры совершенно произволен. На рис. 3 предлагается другой способ деления той же фигуры, которая в этом варианте может быть описана примерно так: две фигуры с выемкой, стоящие на боку и разделенные сверху и снизу двумя распорками, так что вся фигура представляет собой единую конструкцию постоянной ширины.

На рис. 4 показан третий вариант деления фигуры, который можно описать так: две L-образные фигуры положены одна на другую так, что образуют прямоугольник с двумя выступающими плечами, к прямоугольнику приложены два коротких бруска, которые служат продолжением более длинных частей L-образных фигур. Такого рода описание несколько туманно и может привести к недопониманию. Его следует использовать только в том случае, если оба собеседника хорошо знакомы с L-образной конструкцией. Описание любой ситуации зависит от наличия знакомых терминов, с помощью которых наблюдатель хочет ее описать, но это не значит, что выбранный способ описания непременно является наилучшим.

Со временем те части, которые были выделены для облегчения описания или объяснения ситуации, обретают самостоятельное существование. Они продолжают существовать даже тогда, когда ситуация, благодаря которой они возникли, уже забыта. Чем полезнее оказываются они для описания других ситуаций, тем увереннее воспринимаются как самостоятельные сущности.

Тем самым произвольно созданные сущности благодаря своей полезности обретают такую устойчивость, что их реальное существование становится несомненным. Когда процесс доходит до этой стадии, такие сущности могут стать тормозом на пути дальнейшего развития. Чтобы избежать этого, следует постоянно помнить о произвольной природе многих понятий и не допускать их распространения за пределы полезности, ибо только это и дает им право на существование.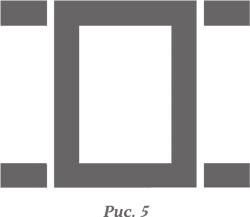

На рис. 5 показан еще один способ деления первоначальной фигуры на составные части. Создается впечатление, что при таком разделении возникают более знакомые элементы, чем в предыдущих вариантах. Однако попытка описать соотношение этих элементов, чтобы их можно было собрать в целостную фигуру, столкнется с серьезными трудностями. Для объяснения недостаточно перечислить имеющиеся элементы, поэтому хорошо знакомыми должны быть не только сами составные части, но и отношения между ними. Часто деление фигуры на наиболее знакомые элементы приводит к тому, что расположение элементов в составе фигуры оказывается, напротив, наименее привычным. Поэтому крайне важно соблюдать баланс между привычностью элементов и привычностью их сочетаний.

Деление неизвестной геометрической фигуры на известные элементы всегда субъективно: знакомые элементы произвольно вычленяются из исходной фигуры. Перед нами не стоит задача непременно открыть именно те элементы, из которых фигура могла быть составлена исходно. Если описание получилось удовлетворительным, то не имеет значения, какой метод деления был при этом выбран.