Загадочное ночное убийство собаки - читать онлайн книгу. Автор: Марк Хэддон cтр.№ 52

И это значит, что нужно найти треугольник, который будет прямоугольным, но стороны которого не могут быть выражены формулами n2 + 1, n2 — 1 и 2n (где n > 1).

Итак, пусть гипотенуза прямоугольного треугольника АВС будет АВ.

Пусть АВ = 65.

Пусть ВС = 60.

Тогда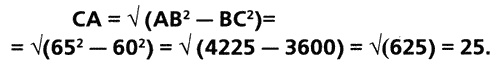

Пусть АВ = n2 +1 = 65.

Тогда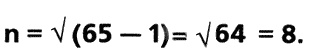

Следовательно,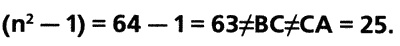

И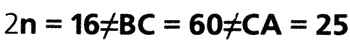

Следовательно, треугольник АВС является прямоугольным, но его стороны не могут быть выражены формулами n2 + 1, n2 — 1 и 2n (где n > 1). Что и требовалось доказать.