Думай «почему?». Причина и следствие как ключ к мышлению - читать онлайн книгу. Автор: Джудиа Перл, Дана Маккензи cтр.№ 98

Предположим, мы хотим узнать эффект воздействия рекламы в Интернете (X) на вероятность того, что потребитель купит товар (Y), скажем доску для серфинга. У нас есть данные, полученные в результате исследований в пяти разных местах — в Лос-Анджелесе, Бостоне, Сан-Франциско, Торонто и Гонолулу. Теперь мы хотим оценить, насколько эффективной эта реклама будет в Арканзасе. К сожалению, все группы и все исследования несколько отличаются. Например, группа, изученная в Лос-Анджелесе, моложе, чем наша целевая аудитория, а в Сан-Франциско она отличается по количеству переходов по ссылке. На рис. 65 показаны уникальные характеристики каждой группы и каждого исследования. Можем ли мы объединить данные, полученные в далеких друг от друга местах, чтобы оценить эффективность рекламы в Арканзасе? Можем ли мы сделать это, не собрав данные в Арканзасе? Или измерив лишь ограниченное число переменных? Или проведя пилотное наблюдательное исследование?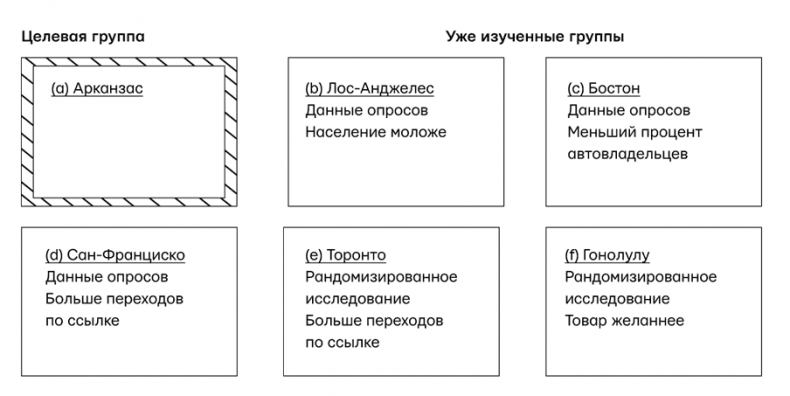

Рис. 65. Проблема транспортабельности

На рис. 66 эти различия переведены в форму графика. Переменная Z представляет возраст, который играет роль осложнителя; молодые люди с большей вероятностью увидят рекламу и с большей вероятностью купят продукт, даже если не видели рекламу. Переменная W отражает переход по ссылке с целью получить дополнительную информацию. Это медиатор — шаг, который необходим, чтобы просмотр рекламы превратился в покупку продукта. Буква S в каждом случае обозначает переменную, «производящую различие», т. е. гипотетическую переменную, которая указывает на характеристики, отличающие две группы. Например, в группе б «Лос-Анджелес» индикатор S указывает на Z, возраст. В каждом из иных городов индикатор указывает на характерную черту группы, приведенную на рис. 65.

Для рекламного агентства хорошая новость здесь в том, что компьютер теперь способен справиться с этой сложной проблемой слияния данных и, руководствуясь do-исчислением, сообщить нам, какие исследования используются для ответа на наш запрос и какими способом это делается, а также какую информацию нам нужно собрать в Арканзасе, чтобы подтвердить вывод. В некоторых случаях эффект переносится напрямую, без дополнительной работы — возможно, нам не придется ехать в Арканзас. Например, эффект от рекламы в Арканзасе должен быть таким же, как в Бостоне, потому что согласно диаграмме, группа с отличается от группы а только переменной V, которая не влияет ни на воздействие X, ни на результат Y.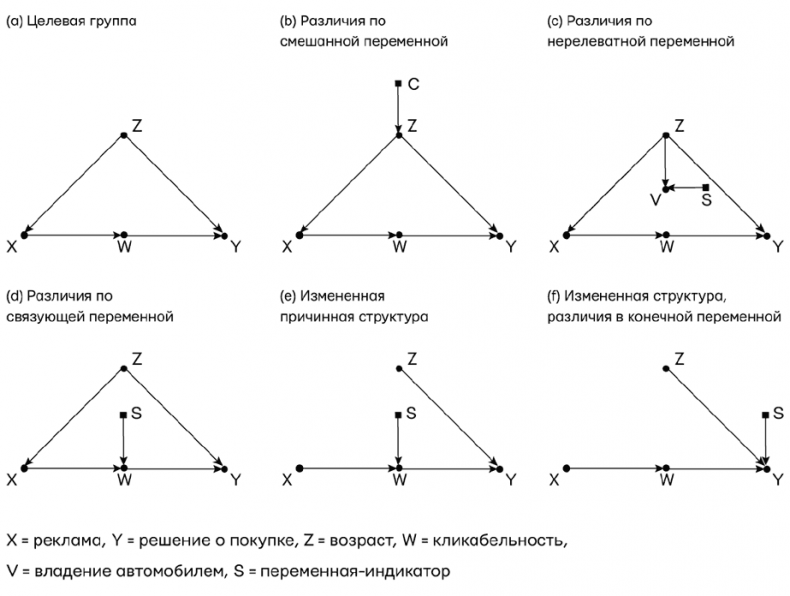

Рис. 66. Различия между исследованными группами, выраженные в графической форме

Нам необходимо по-новому оценить данные в некоторых других исследованиях, положим, принять в расчет иную возрастную структуру населения в лос-анджелесском исследовании б. Интересно, что эксперимента в Торонто e достаточно для оценки нашего запроса в Арканзасе, несмотря на несоответствие в параметре W, если мы можем измерить только X, W и Y в Арканзасе.

Примечательно, что мы нашли примеры, в которых транспортировка невозможна из любого отдельно взятого исследования; тем не менее целевое количество можно оценить по их комбинации. Кроме того, даже исследования, откуда нельзя ничего перенести, не совсем бесполезны. Так, исследование Гонолулу е на рис. 66 невозможно транспортировать из-за стрелки S → Y. Однако стрелка X → W не загрязнена S, поэтому данные, полученные в этой группе, можно использовать для оценки P (W | X). Объединив это с оценками P (W | X) из других исследований, мы повысим точность этого подвыражения. Тщательно комбинируя такие подвыражения, мы можем синтезировать точную общую оценку целевого количества.

Хотя в простых случаях эти результаты интуитивно разумны, когда диаграммы становятся более сложными, нам нужна помощь формального метода. Do-исчисление обеспечивает общий критерий для определения транспортабельности в таких случаях. Правило довольно простое: если выполняется допустимая последовательность do-операций (с использованием правила из главы 7), которые преобразуют целевую величину в другое выражение, в котором любой фактор, включающий S, не содержит do-операторов, тогда оценка транспортабельна. Логика проста: любой такой фактор оценивается по имеющимся данным, не затронутым фактором несоответствия S.

Элиас Баренбойм сумел сделать с проблемой транспортабельности то же, что Илья Шпицер совершил с проблемой интервенции. Он разработал алгоритм, который автоматически определяет, является ли желаемый эффект переносимым, используя только графические критерии. Другими словами, он сообщает, реально ли отделить S от do-операторов или нет.

Результаты Барейнбойма впечатляют, потому что в их свете явление, которое раньше считалось угрозой для валидности, превратилось в новую возможность. Она позволяет нам применять многочисленные исследования, для участников которых нельзя установить собственные критерии (и, соответственно, гарантировать, что исследуемая группа окажется такой же, как интересующая) в наших целях. Вместо того чтобы рассматривать эту разницу как угрозу для внешней валидности исследования, теперь мы устанавливаем валидность в ситуациях, которые раньше казались безнадежными. Именно потому, что мы живем в эпоху больших данных, у нас есть доступ к информации о многих исследованиях и вспомогательных переменных (например, Z и W), которые позволят нам переносить результаты с одной группы на другую.

Попутно упомяну, что Барейнбойм также подтвердил аналогичные результаты для другой проблемы, которая долгое время беспокоила статистиков, — систематической ошибки отбора. Этот вид ошибки возникает, когда изучаемая группа отличается от целевой по какому-либо значимому признаку, что весьма похоже на проблему транспортабельности. Да, эти явления действительно похожи, за исключением одного очень важного отличия: вместо того чтобы рисовать стрелку от индикаторной переменной S к затронутой переменной, мы рисуем стрелку в направлении S. Пусть S обозначает отбор (участников исследования). Скажем, если в нашем исследовании участвовали бы только госпитализированные пациенты, как в примере с ошибкой Берксона, мы бы нарисовали стрелку от госпитализации к S, показывая, что именно она является причиной отбора для нашего исследования. В главе 6 мы рассматривали эту ситуацию только как угрозу для валидности эксперимента. Но теперь получится воспринимать ее как возможность. Если мы поймем механизм, с помощью которого отбираются испытуемые, то преодолеем систематическую ошибку, собрав данные о правильном наборе упростителей и применив соответствующую формулу повторного взвешивания или корректировки. Работа Барейнбойма позволяет нам использовать каузальную логику и большие данные, чтобы творить чудеса, которые раньше были немыслимы.