Думай «почему?». Причина и следствие как ключ к мышлению - читать онлайн книгу. Автор: Джудиа Перл, Дана Маккензи cтр.№ 27

Сам Байес не касался ничего этого в своем тексте; Прайс подчеркнул эти теологические выводы — возможно, чтобы эффект от работы друга был более масштабным. Но оказалось, что Байес не нуждался в помощи. О его работе помнят и ее обсуждают 250 лет спустя, и не из-за теологического значения, а потому, что она показывает: вероятность причины реально вывести из следствия. Если мы знаем причину, легко оценить вероятность следствия — прямую вероятность. Пойти в другом направлении — эту задачу во времена Байеса называли обратной вероятностью — сложнее. Байес не объяснил, почему она сложнее, — он счел это самоочевидным, доказал возможность ее решить и показал нам, как это сделать.

Чтобы оценить суть этой проблемы, давайте рассмотрим пример, который он сам предложил в работе 1763 года, напечатанной посмертно. Представим, что мы делаем удар кием по бильярдному мячу на столе и стараемся, чтобы он отскочил много раз — так, чтобы у нас не было представления о том, где он окажется. Какова вероятность того, что он остановится через X футов от левого края стола? Если мы знаем длину стола и если он абсолютно гладкий и плоский, это очень легкий вопрос (рис. 13а). Так, на 12-футовом столе для снукера вероятность того, что мяч остановится в футе от края, составит. На восьмифутовом бильярдном столе вероятность будет.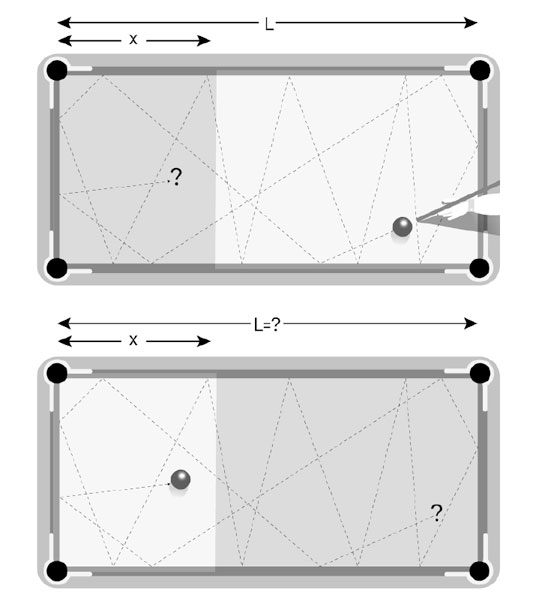

Рис. 13. Пример Томаса Байеса с бильярдным столом: а — в первом варианте, с вопросом о прямой вероятности, мы знаем длину стола и хотим вычислить вероятность того, что шар остановится в x футах от края; б — во втором варианте, с вопросом об обратной вероятности, мы наблюдаем, что шар остановился в x футах от конца и хотим оценить вероятность того, что длина стола составляет L (источник: рисунок Маян Харел)

Интуитивное понимание физики говорит нам, что в общем, если длина стола составляет L футов, вероятность того, что шар остановится в X футах от края составляет x/L. Чем больше длина стола L, тем ниже вероятность, потому что за право зваться конечным положением шара соревнуются больше позиций. Сдругой стороны, чем больше x, тем выше вероятность, поскольку она включает большее число конечных позиций.

Теперь рассмотрим проблему обратной вероятности. Мы наблюдаем конечное положение шара, в котором x = 1 фут от края, но не знаем длины (рис 13б). Преподобный Байес спросил: какова вероятность того, что длина была, скажем, 100 футов? Здравый смысл подсказывает, что длина, вероятнее, составила 50 футов, а не 100, ведь чем длиннее стол, тем труднее объяснить, почему шар оказался так близко к краю. Но насколько это вероятнее? «Интуиция» или «здравый смысл» не дает нам четких указаний.

Почему прямую вероятность (x при известном L) настолько легче оценить в уме, чем вероятность L при известном x? В этом примере асимметрия объясняется тем фактом, что L выступает в роли причины, а x — следствия. Если мы наблюдаем причину, скажем Бобби бросает мяч в окно, большинство может предсказать эффект (мяч, вероятно, разобьет окно). Человеческое познание работает в этом направлении. Но при известном следствии (окно разбито) нам требуется гораздо больше информации, чтобы вывести причину (кто из мальчиков бросил мяч, разбивший окно, или было ли окно вообще разбито мячом). Чтобы учесть все возможные причины, необходим ум Шерлока Холмса. Байес решил удалить эту когнитивную асимметрию и объяснить, как даже обычные люди могут оценить обратную вероятность.

Чтобы посмотреть, как работает метод Байеса, давайте начнем с простого примера о посетителях чайной, о которых у нас есть данные: мы знаем об их предпочтениях. Данные, как нам известно из главы 1, совершенно не в курсе, что существует асимметрия причины и следствия, а значит, с их помощью мы можем найти способ, как разрешить загадку обратной вероятности.

Предположим, что две трети покупателей приходят заказать чай и что половина пьющих чай также заказывают пирожные. Какова будет доля клиентов, которые закажут и чай, и пирожные? В этом вопросе нет подводных камней, и я надеюсь, что ответ почти очевиден.

Поскольку половина двух третей — одна третья, выходит, что одна третья клиентов заказывает чай и пирожные. Чтобы проиллюстрировать это числами, предположим, что мы занесли в таблицу заказы следующих 12 посетителей, которые войдут в дверь.

Как показывает табл. 1, (1, 5, 6, 7, 8, 9, 10, 12) заказали чай и половина из них заказала пирожные (1, 5, 8, 12). Таким образом, доля клиентов, которые заказали и чай, и пирожные действительно равна ½ ∙ =, ровно как мы и предсказывали до того, как увидели конкретные данные.

Таблица 1. Вымышленные данные для примера с чаем и пирожными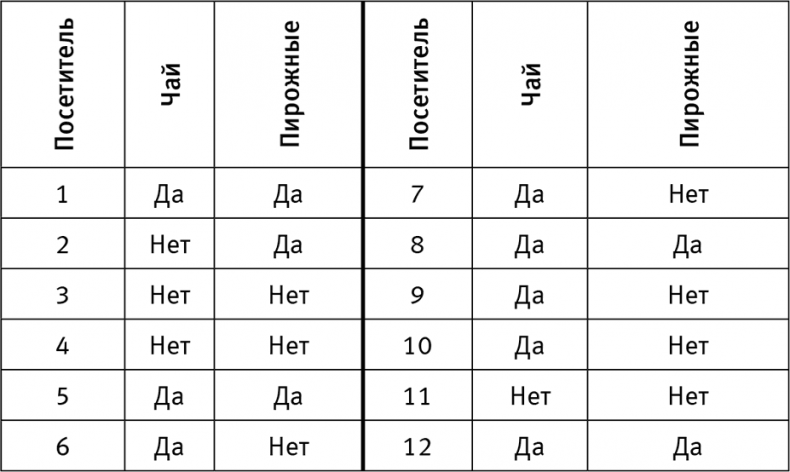

Отправная точка для байесовского правила — заметить, что данные можно было проанализировать в обратном порядке, т. е. мы могли бы заметить, что клиентов (1, 2, 5, 8, 12) заказали пирожные, а из них (1, 5, 8, 12) заказали чай. Таким образом, доля клиентов, которые заказали и чай, и пирожные, будет вычисляться так: ∙ =. Конечно, не случайно у нас получился один и тот же результат; мы просто вычислили одно и то же разными способами. Порядок, в котором клиенты объявляют свои заказы, не играет никакой роли.

Чтобы сделать из этого общее правило, пусть P (T) обозначает вероятность того, что посетитель закажет чай, а P (S) — вероятность того, что он закажет пирожные (помните, что вертикальная линия обозначает «при том что»). Подобным образом, P (T | S) обозначает вероятность заказа посетителем чая при том, что мы уже знаем о заказе им пирожных.

Сначала мы вычисляем следующее:

Второй расчет выглядит так:

Как говорил Евклид 2 300 лет назад, две величины, каждая из которых равна третьей, также равны между собой. Это означает, что справедливо и следующее:

Это безобидное с виду уравнение стало известно как «правило Байеса». Если посмотреть на него внимательнее, то обнаружится, что оно предлагает общее решение для проблемы обратной вероятности. Оно говорит: если мы знаем вероятность S при T, P (S | T), то мы сможем вычислить вероятность T при S, P (T | S) — конечно, при условии, что P (T) и P (S) нам известны. Это, пожалуй, самая важная функция правила Байеса в статистике: мы можем напрямую оценить условную вероятность в одном направлении, где наше суждение надежнее, и применить математику, чтобы получить условную вероятность в другом направлении, для которого наше суждение довольно туманно. Уравнение тоже играет эту роль в байесовских сетях; мы сообщаем компьютеру прямые вероятности, а компьютер выдает обратные вероятности, когда это необходимо.