
|
||
|
|
||
|
|
Онлайн книга - Занимательная экономика. Теория экономических механизмов от А до Я | Автор книги - Александр Филатов , Алексей Савватеев
Cтраница 44

Если это удается сделать без дополнительных потерь, то такие платежи представляют собой простое перераспределение между государством и монополистом, и максимум общественного благосостояния по-прежнему достигается в точке первого наилучшего решения. Однако это идеальная и, как правило, недостижимая на практике ситуация. И дело не только во взятках, распилах или нецелевом использовании средств. Трансакционные издержки никто не отменял, и любое перераспределение богатства внутри общества без них не обходится. На что это влияет? Пусть при предоставлении субсидии в один рубль общество несет дополнительные затраты на сбор и управление средствами в размере λ рублей. Общие затраты на предоставление субсидии в этом случае будут равны (1 + λ). Субсидия призвана вывести естественную монополию из зоны убытков на уровень нулевой прибыли. Следовательно, функция общественного благосостояния представляется как разность потребительского излишка, который записан в виде интеграла, и издержек предоставления субсидии: 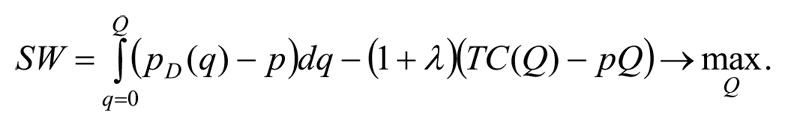
Решение задачи имеет вид 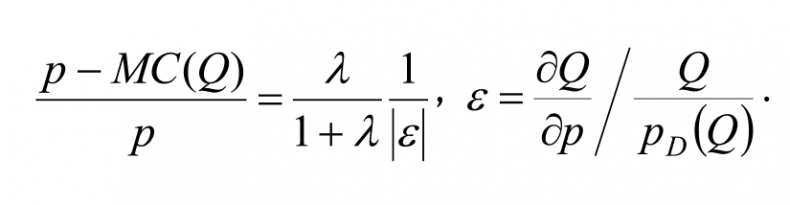
Подобно индексу Лернера, в данной формуле доля наценки в цене пропорциональна обратной эластичности спроса ε, однако здесь присутствует очень важный сомножитель λ / (1 + λ). Если дополнительные издержки на предоставление субсидии отсутствуют (λ = 0), то потребитель платит цену, в точности равную предельным издержкам, и мертвые потери обнуляются. Если же трансакционные издержки присутствуют (λ > 0), то оптимальные цены поднимаются над уровнем MC тем сильнее, чем затратнее оказывается перераспределение, а мертвых потерь не удается избежать полностью. При этом высокий уровень λ может привести к ситуации, когда меньшим из зол окажется переход во второе наилучшее решение, поскольку субсидирование настолько затратно, что его не оправдывает даже рост выпуска и сокращение мертвых потерь. Вторым недостатком субсидирования, который проявляется даже при низком уровне λ, является то, что у фирмы, получающей субсидии, нет никакого стимула к снижению затрат. Напротив, возникает стремление к неоправданному их завышению – ведь все погасится государством. Поэтому данный способ регулирования естественной монополии редко используется на практике. Альтернативным методом, выводящим на первое наилучшее решение, является ценовая дискриминация, о которой уже шла речь в пятой главе книги. В идеальном варианте совершенной ценовой дискриминации монополист продает каждую единицу продукции по своей индивидуальной цене, извлекая при этом весь потребительский излишек. Это, с одной стороны, означает максимально возможный доход производителя, заведомо превышающий даже самые высокие издержки, а с другой – готовность продавать продукцию всем, не отталкивая даже тех потребителей, которые согласны платить только по ценам на уровне предельных затрат. При этом в отсутствие как ограничений, так и компенсационных механизмов производитель сохраняет стимулы к снижению своих издержек, что также повышает эффективность рынка. Конечно, первое наилучшее решение здесь достигается ценой нарушения принципа социальной справедливости – общественное благосостояние целиком достается производителю. Однако в теории снова через налоги или иные механизмы перераспределения пирог может быть разделен между потребителями и монополистом в любой желаемой пропорции. Главное, чтобы его размер был максимален. На практике же совершенная ценовая дискриминация – идеальная картинка, весьма далекая от реальности. Действительно, для ее реализации необходимо точно знать максимальную готовность платить для всех покупателей, после чего создать и внедрить не очень дорогостоящую процедуру назначения для них разных цен, а также исключить возможность перепродажи. Куда более реалистичны схемы ценовой дискриминации второй и третьей степени, реализованные, например, через двухкомпонентные тарифы, включающие плату за доступ, а также блочные тарифы, где цена продукции меняется в зависимости от объема потребления. К их более подробному изложению мы еще вернемся. А пока рассмотрим достаточно важную идею цен Рамсея, которая среди прочего позволяет наиболее эффективным образом осуществить перевод на второе наилучшее решение многопродуктовой монополии. 6.2. Выход на второе наилучшее решение
6.2.1. Цены Рамсея
Задача перевода однопродуктовой фирмы на второе наилучшее решение не представляет особой сложности. Зная кривую спроса на ее продукцию и кривую средних суммарных издержек, регулятор устанавливает тариф на уровне пересечения этих кривых: pD(Q) = ATC(Q). Эта точка соответствует самому высокому уровню выпуска (а значит, и минимальным мертвым потерям), когда производитель не несет убытков, то есть не требует государственных субсидий, с которыми связано множество проблем, обозначенных в предыдущем параграфе. Неслучайно именно этот подход – установить минимальный тариф, при котором монополист не несет убытков, – наиболее часто используется на практике. Однако если естественная монополия производит более одного продукта, то к нулевой прибыли могут привести разные комбинации цен. Действительно, убытки от производства одного вида продукции могут быть компенсированы положительной прибылью от другого. Задача состоит в том, чтобы определить, какая из всех комбинаций цен, обеспечивающих нулевую прибыль, оптимальна с точки зрения общественного благосостояния. Рассмотрим многопродуктовую монополию, которая производит n продуктов в объеме Q = (Q1,…, Qn). Пусть TC(Q) – ее функция суммарных издержек, зависящая от вектора выпуска Q, MCi(Q) = ∂TC(Q) / ∂Qi – предельные издержки производства i-го продукта, pi (Q) – обратная функция спроса для i-го продукта. Заметим вновь, что готовность платить за i-й продукт в общем случае зависит от всего вектора выпуска, равно как и функция издержек в общем случае является несепарабельной. Тогда задача максимизации общественного благосостояния при условии нулевой прибыли монополиста выглядит следующим образом: 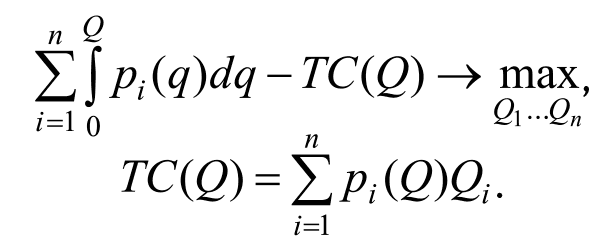
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно