
|
||
|
|
||
|
|
Онлайн книга - Занимательная экономика. Теория экономических механизмов от А до Я | Автор книги - Александр Филатов , Алексей Савватеев
Cтраница 21

Кстати, вопрос, связанный с эффективностью, не вполне очевиден – ведь максимальную ставку может сделать участник аукциона с немаксимальной оценкой. Однако такое может произойти лишь в несимметричном равновесии, когда разные участники пользуются разными стратегиями, а это мы запретим чуть ниже. Также тут неявно кроется требование о том, что объект ни при каких заявках участников не остается в руках аукциониста при условии, что для последнего он не имеет никакой ценности. В частности, такое требование исключает использование резервной цены, начиная с которой идут торги: ведь при наличии порогового значения существуют реализации оценок участников, при которых объект не будет продан. Второе требование, отсутствие входного билета, заключается в том, что человек с нулевой оценкой может заявить ноль и остаться при своих. Формально требование должно быть выполнено в среднем, то есть ожидаемый платеж игрока с нулевой ставкой равен нулю. Однако при дополнительном ограничении, что участникам ни при каких обстоятельствах не выплачивают никаких денег, усредненный ноль означает ноль при любых условиях. Точнее, как говорят математики, «почти всегда» – на множестве реализаций, имеющем полную меру. Независимо от распределения оценок и ставок всех остальных участников аукциона, участник, заявивший ноль, платит ноль. Последнее условие, которое необходимо для справедливости теоремы Майерсона об эквивалентности форматов, заключается в том, что участники аукциона используют одинаковые стратегии ведения борьбы за объект. Иными словами, теорема о равенстве доходов аукциониста при разных форматах проведения аукциона верна при разыгрывании симметричного равновесия. 3.2.2. Доказательство теоремы Майерсона
Докажем теорему Майерсона об эквивалентности форматов. Для этого введем следующие обозначения. Пусть vi – это оценка i-го участника аукциона. Она является случайной величиной, которая распределена регулярным образом (то есть имеет математическое ожидание и дисперсию) на множестве неотрицательных чисел. Пусть также bi – это ставка i-го участника. Равновесную стратегию игроков обозначим за s (•). Обращаем внимание: мы сразу же рассматриваем именно равновесную стратегию, опуская весь процесс ее нахождения! Функцию распределения оценок (то есть типов участников) обозначим за F (•), и в силу симметрии она будет одна и та же для всех – все участники аукциона принципиально неотличимы друг от друга. Априори, то есть до начала проведения аукциона, все n случайных величин v1,…, vn распределены независимым образом и неизвестны участникам, однако после показа лота каждый участник узнаёт свое собственное значение vi. Теперь применим следующий трюк. Обозначим за M (v) функцию, определяющую ожидаемый в рассматриваемом равновесии s (•) платеж игрока, узнавшего свою оценку v. Таким образом, игрок (и мы вслед за ним) должен усреднить результат своего участия с данной оценкой по множеству всех наборов реализаций оценок прочих участников, то есть на пространстве размерности (n – 1). Так как все прочие оценки независимы друг от друга, то вопрос сводится к взятию (n – 1) – кратного интеграла по этому множеству как раз от функции платежа m (которая определяется при любых конкретных реализациях правилами аукциона), примененной к набору {s (vj)}, домноженной на совместную плотность распределения. Последняя, в силу независимости случайных величин, равна произведению плотностей f (vj) в соответствующих точках vj, определяющих реализации оценок остальных участников. С какой вероятностью предмет достанется участнику с оценкой v? В силу требования эффективности аукциона это произойдет в том и только том случае, когда заявка нашего игрока s (v) перебьет все прочие заявки s (vj). Теперь вступает в игру монотонность функции s (•), одинаковой для всех игроков равновесной стратегии участия. Монотонность позволяет заключить, что участник с оценкой v победит в аукционе и получит предмет только в том случае, когда его оценка окажется максимальной. Таким образом, вероятность победы для участника с оценкой v равняется F n–1 (v). Чтобы окончательно абстрагироваться от всей лишней информации, обозначим теперь функцию F n–1 (•) за G (•). Сразу же заметим, что она определяется только тем, как именно априорно распределены оценки участников, а не тем, как устроен наш аукцион и какое именно симметричное равновесие s (•) мы рассматриваем. Если вдруг для данного формата окажется несколько равновесных стратегий, выводы будут одни и те же. Переходим к ключевому моменту. Если участник с оценкой v следует стратегии s (•), то он получает предмет с вероятностью G (v) и платит в среднем M (v). Таким образом, его ожидаемый выигрыш в этой игре равен: vG (v) – M (v). Если же он изменит поведение, вместо s (v) заявив, то это фактически эквивалентно тому, что он прикинется участником с оценкой. По крайней мере это верно в том случае, если выпавшая оценка v – не краевая, то есть не равна ни нулю, ни максимальной возможной оценке (в случае, когда диапазон всех оценок является каким-то конечным отрезком [0, T]), и если отклонение окажется незначительным, не выводящим оценку за пределы допустимого диапазона. Что получит игрок с оценкой v, если он прикинется игроком с оценкой, близкой к v? Он получит лот с вероятностью G(), заплатив в среднем M(). Так как лот на самом деле имеет для него ценность v, то выигрыш будет равен: 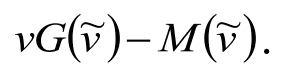
Такое изменение должно быть невыгодно, поскольку стратегия участия s (•) – равновесная, и поэтому она является оптимальным ответом на себя саму. То есть при условии, что остальные участники следуют этой стратегии, заявка s (v) должна доставлять максимум функции ожидаемого выигрыша участника с оценкой v. Таким образом, при любых должно быть выполнено неравенство: 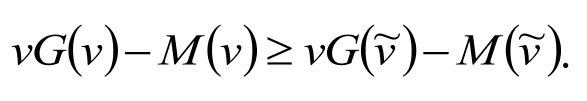
Для дифференцируемых функций из этого следует, что производная по от функции обращается в ноль именно в точке v, иначе даже локального максимума нам не получить, то есть 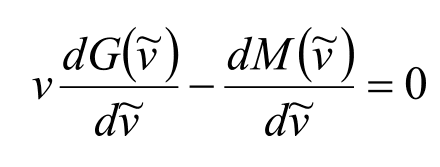
|
 Вернуться к просмотру книги
Вернуться к просмотру книги
 Перейти к Оглавлению
Перейти к Оглавлению
 © 2020 LoveRead.ec - электронная библиотека в которой можно
© 2020 LoveRead.ec - электронная библиотека в которой можно