Лаборатория химических историй. От электрона до молекулярных машин - читать онлайн книгу. Автор: Михаил Левицкий cтр.№ 64

Отойдем в сторону от химии и посмотрим, как находят нужное решение, например, музыканты. Познакомимся со случаем, когда художник не сам ставит себе задачу, а она дается уже в сформулированном виде, что выглядит как некоторое "насилие над творческой личностью". В одном из интервью композитор Р. Щедрин рассказывал, что в 1999 г. ему позвонили из Нюрнберга и предложили написать вступление к Девятой симфонии Бетховена. Тот же самый состав оркестра и те же самые музыканты должны исполнять без перерыва вступление и саму симфонию. Безусловно, задача была необычайно трудная и очень ответственная. Решение пришло к композитору в тот момент, когда во время движения по шоссе его машина забуксовала на льду и съехала в кювет. Вместе с чувством крайнего раздражения и досады родилась нужная идея. Ее воплощение, по мнению автора, является лучшим из всего, что он написал в 1999 г. Рекламная подача описанного события сделает упор на минутную потерю управления автомобилем, но спокойные рассуждения приводят нас к иному. Главное – то, что композитор долго и упорно размышлял, а дорожное происшествие просто сыграло роль "спускового крючка".

Трудный путь, ведущий к озарению, у большинства творческих людей, по-видимому, достаточно похож. Высказывания талантливых людей, далеких от науки, подтверждают это: "Поэзия – та же добыча радия…" (В. В. Маяковский); "Талант – это труд, упорный и повседневный" (А. П. Чехов). За всеми этими высказываниями скрыта одна важная деталь. Упорный труд творческого человека совершается не по принуждению, а в силу естественной потребности пытливого ума во что бы то ни стало решить поставленную задачу.

Отыскать точный путь, ведущий к цели, принять правильное решение, найти компромисс между желаемым и достижимым – подобные проблемы возникают как в жизни, так и в науке, в том числе и в химии. Оказывается, что в подобных случаях может помочь математика.

Три женщины решили совместно купить один большой кусок мяса. Каждая внесла по 100 рублей. На общую сумму 300 руб. было куплено мясо, и далее встал вопрос о том, как его разделить. Дело в том, что крупный кусок мяса всегда неоднороден. В одном месте косточка, одна часть более мягкая, другая более жилистая. Следовательно, по весу делить нельзя. Одна из женщин сказала, что берется разрезать этот кусок на три части, равные по стоимости, то есть каждый кусок будет стоить 100 рублей. Она разрезала мясо и сказала: «Ручаюсь, что все три куска имеют равную стоимость». Вторая женщина, поглядев на получившиеся куски, сказала, что, с ее точки зрения, один кусок действительно стоит 100 руб., другой, по ее мнению, стоит 80 руб., а третий – 120 руб. Она просто высказала свои соображения, но не указала на конкретные куски. Третья женщина сказала, что оценивает все иначе, и более ничего не уточняла. Задача состоит в том, чтобы, ничего более не разрезая, раздать куски так, чтобы все три женщины остались довольны. Задача эта, как вы понимаете, несложная, вариантов раздачи кусков не так много. Однако некоторые рассуждения необходимы. Для наглядности изобразим условия задачи в виде таблицы (рис. 10.1).

Ясно, что первой женщине можно оставить любой из трех кусков, так как она утверждает, что все они равноценны. Дать право первого выбора второй женщине нельзя. Может получиться, что после того, как вторая женщина выберет себе кусок мяса, третья женщина скажет, что каждый из оставшихся кусков стоит меньше 100 руб., так как мы не знакомы с ее оценками. Но одно мы можем утверждать с уверенностью. Не может быть так, чтобы, с точки зрения третьей женщины, каждый кусок стоил меньше 100 руб., иначе она просто не согласилась бы на эту покупку. Следовательно, хотя бы один кусок должен ее удовлетворить.

Итак, единственный выход – дать право первого выбора третьей женщине. Даже если она возьмет тот кусок, который, с точки зрения второй женщины, стоит 120 руб., то для второй женщины остается возможность взять кусок, который, с ее точки зрения, стоит 100 руб. Ну а первой женщине достается оставшийся кусок, и это должно ее устроить, ведь она считает, что все куски равноценны.

Таким образом, задача решена. Справедливое ли такое решение? Назовем его наполовину справедливым. Вполне может случиться, что вторая женщина, получив кусок стоимостью 100 руб., будет раздражена тем, что третьей достался кусок стоимостью (с ее точки зрения) выше 100 руб.

Практичному рассудительному человеку подобные эмоции неведомы. Его волнует, чтобы справедливость была соблюдена только по отношению к нему, то есть он должен получить кусок стоимостью не меньше 100 руб. Однако в жизни встречаются люди различного темперамента. Поэтому будем называть справедливым разделом такую систему, при которой каждый получает больше, чем он рассчитывал, то есть справедливость "с довеском". Неужели такое возможно? Это веет нарушением закона сохранения материи. Тем не менее во многих случаях это осуществимо, и математика предлагает варианты подобных решений.

Три брата получили в наследство старинную гитару, видеокамеру, каминные часы и акваланг. С самого начала они договорились разделить наследство поровну, что, кстати, вполне соответствует юридическим нормам деления наследства между братьями. Продавать все эти вещи и делить полученные деньги они не хотят, так как обычно вещи продаются по цене ниже реальной стоимости. В похожих случаях можно применять универсальную схему. Каждый брат независимо от других указывает свою цену для каждой вещи. Представим все в виде таблицы – оценка наследства в рублях, проведенная каждым братом, показана на рис. 10.2.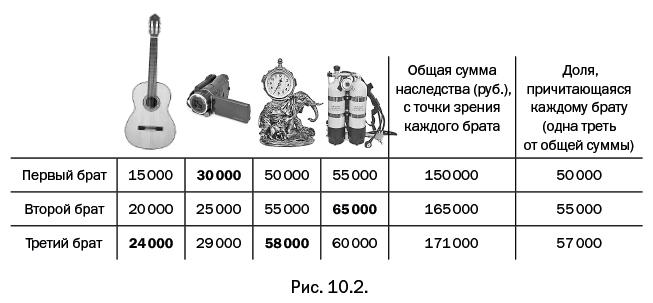

Далее, в соответствии с правилами этой схемы, каждый из братьев получает ту вещь, которую он оценил дороже, чем другие. Соответствующие цифры в таблице выделены жирным шрифтом. Итак, видеокамера достается первому брату, акваланг – второму брату, а гитара и часы – третьему брату.

Первый брат:

рассчитывал получить свою долю – 50 000 руб. (см. последний столбец в таблице);

получил видеокамеру – 30 000 руб. Пока что он получил меньше того, на что рассчитывал.

Теперь второй брат:

рассчитывал получить 55 000 руб.;

получил акваланг стоимостью 65 000 руб.

Разницу 65 000 – 55 000 = 10 000 руб. в виде денежных купюр он должен положить на стол.

Далее третий брат: